Cho hàm số \(y = \sqrt {5 - 4x} \) trên đoạn \(\left[ { - 1;1} \right]\).
a) Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = \sqrt 5 \) và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = 0\).
b) Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = 1\) và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = - 3\).
c) Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = 3\) và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = 1\).
d) Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = 0\) và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = - \sqrt 5 \).
Cho hàm số \(y = \sqrt {5 - 4x} \) trên đoạn \(\left[ { - 1;1} \right]\).
a) Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = \sqrt 5 \) và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = 0\).
b) Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = 1\) và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = - 3\).
c) Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = 3\) và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = 1\).
d) Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = 0\) và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = - \sqrt 5 \).
Quảng cáo
Trả lời:
Điều kiện xác định: \(5 - 4x \ge 0 \Leftrightarrow x \le \frac{5}{4}\). Ta có \(y' = \frac{{ - 2}}{{\sqrt {5 - 4x} }} < 0,\forall x \in \left[ { - 1;1} \right]\).
Do đó \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = y\left( { - 1} \right) = 3\) và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = y\left( 1 \right) = 1\).
Đáp án: a) Sai; b) Sai; c) Đúng; d) Sai
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(\mathop {\max }\limits_{\left[ { - 2;2} \right]} y = - 1\); \(\mathop {\min }\limits_{\left[ {0; + \infty } \right)} y = - 5\).
Không tồn tại giá trị nhỏ nhất của hàm số trên \(\left( { - \infty ;1} \right]\).
\(\mathop {\min }\limits_{\left[ { - 1;2} \right]} y = y\left( 1 \right) = - 5\).
Đáp án: a) Đúng; b) Đúng; c) Sai; d) Đúng
Lời giải
Gọi hai kích thước của hình chữ nhật là \(x\) và \(y\), với \(2x + y = 240\) \(\left( {0 < x < 120;0 < y < 240} \right)\).
Suy ra \(y = 240 - 2x\).
Diện tích của mảnh vườn hình chữ nhật là:
\(S = xy = x\left( {240 - 2x} \right) = 240x - 2{x^2},0 < x < 120\).
\(S' = 240 - 4x\); \(S' = 0 \Leftrightarrow x = 60 \in \left( {0;120} \right)\)
Bảng biến thiên
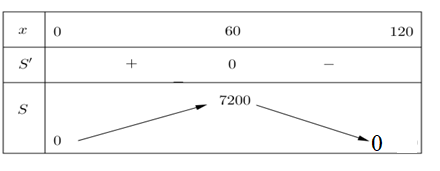
Từ bảng biến thiên ta thấy \(\mathop {\max }\limits_{\left( {0;120} \right)} S = 7200 \Leftrightarrow x = 60\).
Trả lời: 7200.
Câu 3
A.\[2.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
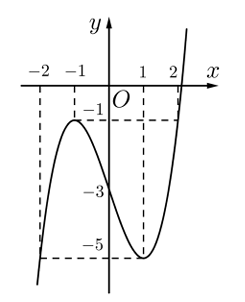
![Từ đồ thị ta có: \[\left\{ \begin{array}{l}m = \mathop {\min }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( { - 2} \right) = - 4\\M = \mathop {\max }\limits_{\left[ { - 1 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/10-1761388534.png)