Cho hàm số \(y = x - \frac{1}{{x + 1}}\)
a) Đồ thị của hàm số có tiệm cận đứng là \(x = 1\).
b) Đồ thị hàm số cắt trục \(Oy\) tại \(M\). Phương trình tiếp tuyến của tại \(M\) là \(y = 2x - 1\).
c) Tồn tại hai tiếp tuyến của đồ thị vuông góc với nhau.
d) Để đường thẳng \(y = k\) cắt \((C)\) tại hai điểm phân biệt \(A\) và \(B\) sao cho \(OA \bot OB\) khi đó \(k\) là nghiệm của phương trình \({k^2} - k - 1 = 0\).
Cho hàm số \(y = x - \frac{1}{{x + 1}}\)
a) Đồ thị của hàm số có tiệm cận đứng là \(x = 1\).
b) Đồ thị hàm số cắt trục \(Oy\) tại \(M\). Phương trình tiếp tuyến của tại \(M\) là \(y = 2x - 1\).
c) Tồn tại hai tiếp tuyến của đồ thị vuông góc với nhau.
d) Để đường thẳng \(y = k\) cắt \((C)\) tại hai điểm phân biệt \(A\) và \(B\) sao cho \(OA \bot OB\) khi đó \(k\) là nghiệm của phương trình \({k^2} - k - 1 = 0\).
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
|
a) |
S |
b) |
Đ |
c) |
S |
d) |
Đ |
Sai: \(y = x - \frac{1}{{x + 1}}\). Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)
Đạo hàm \(y' = 1 + \frac{1}{{{{(x + 1)}^2}}} > 0,\forall x \in D\): hàm số luôn luôn đồng biến, không có cực đại, cực tiểu.
\(\mathop {\lim }\limits_{x \to - 1 \mp } y = \pm \infty :x = - 1\)là tiệm cận đứng
\(\mathop {\lim }\limits_{x \to \pm \infty } y = x:y = x\)là tiệm cận xiên
Đúng: \(M\left( {0;\, - 1} \right),y'\left( 0 \right) = 2\)
Phương trình tiếp tuyến \(\left( T \right)\) tại \(M:y = 2\left( {x - 0} \right) - 1 \Leftrightarrow y = 2x - 1\)
Sai: Tiếp tuyến \(\left( {{T_1}} \right)\) của \((C)\) tại \(P\left( {{x_1},{y_1}} \right)\) có hệ số góc \({k_1} = {y'_{{x_1}}} = 1 + \frac{1}{{{{\left( {{x_1} + 1} \right)}^2}}} > 0\)
Tiếp tuyến \(\left( {{T_2}} \right)\) của \((C)\) tại \(Q\left( {{x_2},{y_2}} \right)\) có hệ số góc \({k_2} = {y'_{{x_2}}} = 1 + \frac{1}{{{{\left( {{x_2} + 1} \right)}^2}}} > 0\)
Do \({y'_{{x_1}}} > 0,\,{y'_{{x_2}}} > 0\) nên không thể có 2 tiếp tuyến của \(\left( C \right)\) vuông góc nhau
Đúng: \(y = x - \frac{1}{{x + 1}} = \frac{{{x^2} + x - 1}}{{x + 1}}\)
Phương trình hoành độ giao điểm của \(\left( C \right)\) và đường thẳng \(y = k\):
\(\frac{{{x^2} + x - 1}}{{x + 1}} = k \Leftrightarrow \left\{ \begin{array}{l}x \ne - 1\\{x^2} - \left( {k - 1} \right)x - \left( {k + 1} \right) = 0\,\,\,\,\,\left( * \right)\end{array} \right.\)
Do vị trí của \(\left( C \right)\) trên hệ tọa độ \(Oxy\) có thể kết luận \(\left( * \right)\) luôn có 2 nghiệm phân biệt \({x_A},{x_B} \ne - 1\) và \(\left\{ {\begin{array}{*{20}{l}}{{x_A} + {x_B} = k - 1}\\{{x_A}.{x_B} = - \left( {k + 1} \right)}\end{array};\,\,A\left( {{x_A};k} \right),B\left( {{x_B};k} \right)} \right.\)
\(\begin{array}{l}\overrightarrow {OA} = \left( {{x_A},k} \right),\overrightarrow {OB} = \left( {{x_B},k} \right)\\OA \bot OB \Leftrightarrow \overrightarrow {OA} \cdot \overrightarrow {OB} = 0 \Leftrightarrow {x_A}{x_B} + {k^2} = 0 \Leftrightarrow - k - 1 + {k^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{k = \frac{{1 - \sqrt 5 }}{2}}\\{k = \frac{{1 + \sqrt 5 }}{2}}\end{array}} \right.\end{array}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
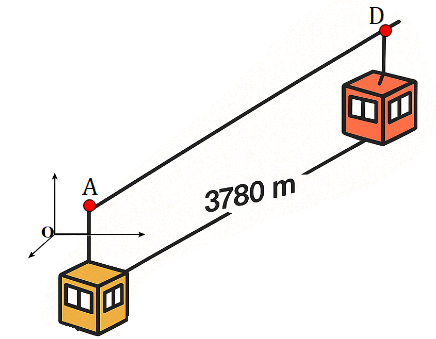
Gọi tọa độ điểm \(B\left( {550;\,y;\,z} \right)\).
Ta có: \(\overrightarrow {AB} = \left( {540;\,y - 3;\,z} \right)\).
Do đường đi của cabin cùng phương với vectơ \(\vec u = \left( {2;\, - 2;\,1} \right)\) nên ta có:
\(\frac{{540}}{2} = \frac{{y - 3}}{{ - 2}} = \frac{z}{1}\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y - 3 = - 540}\\{z = 270\,\,\,\,\,\,\,\,\,}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = - 537}\\{z = 270}\end{array}} \right.\)\( \Rightarrow B\left( {550;\, - 537;\,270} \right)\).
Quãng đường \(AB\) bằng \(AB = \sqrt {{{540}^2} + {{\left( { - 537 - 3} \right)}^2} + {{270}^2}} = 810\).
Vận tốc của cabin bằng \(v = \frac{{AB}}{{3.60}} = 4,5\,\left( {{\rm{m/s}}} \right)\).
Thời gian để cabin chuyển động đều từ điểm \(A\) đến điểm \(D\) là: \(\frac{{3780}}{{4,5}} = 840\).
Câu 2
Một giỏ hoa treo trong nhà làm bằng 3 sợi dây không giãn, mỗi sợi dài \(60\left( {cm} \right)\) miếng kê là một miếng gỗ cân đối hình tròn bán kính \(20\left( {cm} \right)\), ba sợi dây được thắt một đầu bên trên và đỡ giá gỗ tại 3 điểm tạo thành tam giác đều . Biết lực chịu đựng của mỗi sợi dây bằng nhau và mỗi sợi chịu không quá \(15N\) trọng lượng của miếng giá gỗ là \(5N\). Tính trọng lượng tối đa của các chậu hoa để dây treo không bị đứt .

Một giỏ hoa treo trong nhà làm bằng 3 sợi dây không giãn, mỗi sợi dài \(60\left( {cm} \right)\) miếng kê là một miếng gỗ cân đối hình tròn bán kính \(20\left( {cm} \right)\), ba sợi dây được thắt một đầu bên trên và đỡ giá gỗ tại 3 điểm tạo thành tam giác đều . Biết lực chịu đựng của mỗi sợi dây bằng nhau và mỗi sợi chịu không quá \(15N\) trọng lượng của miếng giá gỗ là \(5N\). Tính trọng lượng tối đa của các chậu hoa để dây treo không bị đứt .

Lời giải
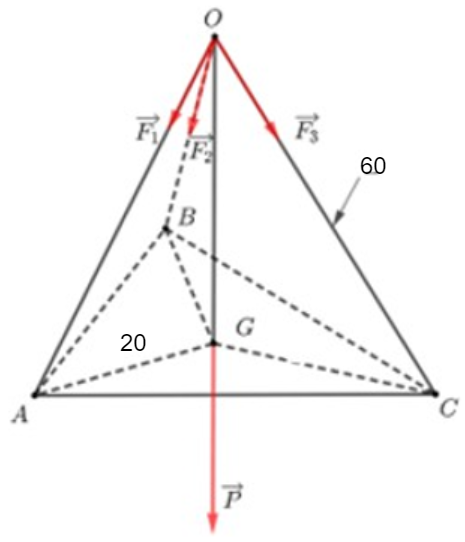
Gọi điểm thắt một đầu bên trên là \[O\] và \[3\] điểm nối \[3\] sợi dây với giá gỗ tạo thành tam giác đều \[ABC\]. Gọi \[G\] là trọng tâm tam giác \[ABC\].
Vì tam giác \[ABC\] đều nên \[G\] là tâm đường tròn ngoại tiếp tam giác \[ABC\].
Do đó, \[GA = GB = GC = 20cm\]. Gọi \[F\] là độ lớn của các lực căng \[{F_1},{F_2}\;,{F_3}\] trên mỗi sợi dây. Đặt \[F = \;x\] với \[0 < x \le 15\].
Theo bài ra ta có \[OA = OB = OC = 60cm\] nên \[OG \bot \left( {ABC} \right)\] và \[\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right| = \left| {\overrightarrow {OC} } \right| = 60\]
Do đó, \[\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|\]. Từ đó ta có \[\overrightarrow {{F_1}} = \frac{x}{{60}}\overrightarrow {OA} , \overrightarrow {{F_2}} = \frac{x}{{60}}\overrightarrow {OB} , \overrightarrow {{F_3}} = \frac{x}{{60}}\overrightarrow {OC} \].
Suy ra \[\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \frac{x}{{60}}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{{3x}}{{60}}\overrightarrow {OG} = \frac{x}{{20}}\overrightarrow {OG} \].
Mặt khác, ta lại có \[\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \] với \[\overrightarrow P \] là trọng lượng của giá gỗ và các chậu hoa.
Nên ta có \[\left| {\overrightarrow P } \right| = \frac{x}{{20}}\left| {\overrightarrow {OG} } \right| = \frac{{x\sqrt {{{60}^2} - {{20}^2}} }}{{20}} = x\sqrt 8 \le 15\sqrt 8 \].
Vậy giá trị lớn nhất trọng lượng giá gỗ và chậu hoa là \[\max \left| {\overrightarrow P } \right| = 15\sqrt 8 .\]
Suy ra trọng lượng tối đa của các chậu hoa để dây treo không bị đứt là \[15\sqrt 8 - 5 \approx 37,4\left( N \right)\].
Câu 3
Giả sử chiều cao của một giống cây trồng tuân theo quy luật logistic được mô hình hoá bằng hàm số \(f\left( t \right) = \frac{{200}}{{1 + 4{e^{ - t}}}},\;\;t \ge 0\). Trong đó thời gian \(t\) được tính bằng tháng kể từ khi hạt bắt đầu nảy mầm. Khi đó đạo hàm \(f'\left( t \right)\) sẽ biểu thị tốc độ tăng chiều cao của giống cây đó. Hỏi sau khi hạt giống bắt đầu nảy mầm thì sau bao nhiêu tháng tốc độ tăng chiều cao của cây là lớn nhất?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho một tấm nhôm hình lục giác đều cạnh \[90\] cm. Người ta cắt ở (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/21-1761612074.png)