Vận tốc của một tàu con thoi từ lúc cất cánh tại thời điểm \[t = 0\,\,\left( s \right)\] cho đến thời điểm \[t = 126\,\,\left( s \right)\] được cho bởi công thức \[v(t) = 0,001302{t^3} - 0,09029{t^2} + 83\] (vận tốc được tính bằng đơn vị \[ft/s\]). Hỏi tại thời điểm tàu con thoi đạt gia tốc nhỏ nhất thì vận tốc tàu con thoi gần bằng bao nhiêu? (Kết quả làm tròn đến hàng phần mười).
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Ta có: \[a\left( t \right) = v'(t) = 0,003906{t^2} - 0,18058t\]
Ta có BBT hàm \[a\left( t \right) = 0,003906{t^2} - 0,18058t\].
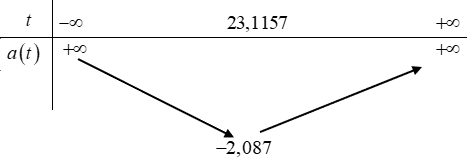
Thời điểm tàu con thoi đạt gia tốc nhỏ nhất là \[t \approx 23,1157\]
\[v(23,1157) = 0,001302{t^3} - 0,09029{t^2} + 83 \approx 20,8\]ft/s
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) |
S |
b) |
S |
c) |
Đ |
d) |
S |
(b) Sai: \(\left| {\vec u\left| = \right|\vec v} \right| \Leftrightarrow \sqrt {13} = \sqrt {{{\left( {m - 1} \right)}^2} + 4{m^2} + 9} \Leftrightarrow 5{m^2} - 2m - 3 = 0 \Leftrightarrow m = 1\) hoặc \(m = - \frac{3}{5}\).
(c) Đúng: Khi \(m = 1\) thì \(\vec v = \left( {0;2;3} \right)\). Suy ra \(\vec u = \vec v\).
(d) Sai: \(\vec u \bot \vec u \Leftrightarrow 4m + 9 = 0 \Leftrightarrow m = - \frac{9}{4}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.