Cho phương trình \(\left( {2\sin x - 1} \right)\left( {3\cos 2x + 2\sin x - m} \right) = 3 - 4{\cos ^2}x\). Tìm tất cả các giá trị của tham số \(m\) để phương trình có đúng ba nghiệm phân biệt trên đoạn \(\left[ { - \frac{\pi }{4};\frac{\pi }{4}} \right]\).
Cho phương trình \(\left( {2\sin x - 1} \right)\left( {3\cos 2x + 2\sin x - m} \right) = 3 - 4{\cos ^2}x\). Tìm tất cả các giá trị của tham số \(m\) để phương trình có đúng ba nghiệm phân biệt trên đoạn \(\left[ { - \frac{\pi }{4};\frac{\pi }{4}} \right]\).
Câu hỏi trong đề: Bộ 10 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải:
Ta có \(\left( {2\sin x - 1} \right)\left( {3\cos 2x + 2\sin x - m} \right) = 3 - 4{\cos ^2}x\)
\( \Leftrightarrow \left( {2\sin x - 1} \right)\left( {3\cos 2x + 2\sin x - m} \right) = 4{\sin ^2}x - 1\)
\[ \Leftrightarrow \left( {2\sin x - 1} \right)\left( {3\cos 2x + 2\sin x - m} \right) = \left( {2\sin x - 1} \right)\left( {2\sin x + 1} \right)\]
\[ \Leftrightarrow \left( {2\sin x - 1} \right)\left[ {\left( {3\cos 2x + 2\sin x - m} \right) - \left( {2\sin x + 1} \right)} \right] = 0\]
\[ \Leftrightarrow \left( {2\sin x - 1} \right)\left[ {3\cos 2x - \left( {m + 1} \right)} \right] = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}2\sin x - 1 = 0\\3\cos 2x - \left( {m + 1} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sin x = \frac{1}{2}\\\cos 2x = \frac{{m + 1}}{3}\end{array} \right.\]
Xét \(\sin x = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{6} + k2\pi \end{array} \right.,k \in \mathbb{Z}\). Khi đó trong khoảng \(\left[ { - \frac{\pi }{4};\frac{\pi }{4}} \right]\) có 1 nghiệm \(x = \frac{\pi }{6}\). Như vậy, để phương trình có 3 nghiệm nằm trong khoảng \(\left[ { - \frac{\pi }{4};\frac{\pi }{4}} \right]\) thì phương trình \[\cos 2x = \frac{{m + 1}}{3}\] có 2 nghiệm khác \(\frac{\pi }{6}\) trong khoảng \(\left[ { - \frac{\pi }{4};\frac{\pi }{4}} \right]\).
Xét hàm số \(y = \cos 2x\) trong khoảng \(\left[ { - \frac{\pi }{4};\frac{\pi }{4}} \right]\) có bảng biến thiên như sau:
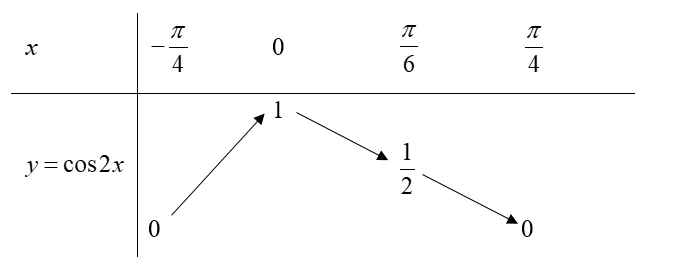
Như vậy, để phương trình \[\cos 2x = \frac{{m + 1}}{3}\] có 2 nghiệm phân biệt khác \(\frac{\pi }{6}\) thì:
\(\left\{ \begin{array}{l}0 \le \frac{{m + 1}}{3} < 1\\\frac{{m + 1}}{3} \ne \frac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 1 \le m < 2\\m \ne \frac{1}{2}\end{array} \right.\).
Vậy \(m \in \left[ { - 1;2} \right)\backslash \left\{ {\frac{1}{2}} \right\}\) thoả mãn đề bài.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải:
a) Ta có: \({v_n} = {u_n} + 3 \Rightarrow {v_{n + 1}} = {u_{n + 1}} + 3\)
Xét \(\frac{{{v_{n + 1}}}}{{{v_n}}} = \frac{{{u_{n + 1}} + 3}}{{{u_n} + 3}} = \frac{{4{u_n} + 9 + 3}}{{{u_n} + 3}} = \frac{{4\left( {{u_n} + 3} \right)}}{{{u_n} + 3}} = 4 \Rightarrow \left( {{v_n}} \right)\) là một cấp số nhân với công bội \(q = 4\) và \({v_1} = {u_1} + 3 = 2 + 3 = 5\).
\( \Rightarrow {v_n} = {v_1}.{q^{n - 1}} = {5.4^{n - 1}}\).
Vậy cấp số nhân \(\left( {{v_n}} \right)\) có số hạng tổng quát \({v_n} = {5.4^{n - 1}}\).
b) Gọi \[{T_n}\] là tổng của \(n\) số hạng đầu tiên của cấp số nhân \(\left( {{v_n}} \right)\) và \({S_n}\) là tổng của \(n\) số hạng đầu tiên của dãy số \(\left( {{u_n}} \right)\). Khi đó \({T_n} = {v_1} + {v_2} + ... + {v_n}\) và \({S_n} = {u_1} + {u_2} + ... + {u_n}\).
Ta có: \({T_n} = {v_1} + {v_2} + ... + {v_n} = \left( {{u_1} + 3} \right) + \left( {{u_2} + 3} \right) + ... + \left( {{u_n} + 3} \right)\)
\( = \left( {{u_1} + {u_2} + ... + {u_n}} \right) + 3n = {S_n} + 3n\)
\( \Rightarrow {S_n} = {T_n} - 3n\)
\( \Rightarrow {S_{10}} = {T_{10}} - 3.10 = \frac{{{v_1}\left( {1 - {q^{10}}} \right)}}{{1 - q}} - 3.10 = \frac{{5\left( {1 - {4^{10}}} \right)}}{{1 - 4}} - 30 = 1747595\).
Vậy tổng 10 số hạng đầu tiên của \(\left( {{u_n}} \right)\) là 1 747 595.
Lời giải

a) Trong mặt phẳng \(\left( {ABCD} \right)\), gọi \(E\) là giao điểm của \(AC\) và \(BI\), khi đó \(SE\) nằm trên mặt phẳng \(\left( {SAC} \right)\).
Mà \(IJ\) và \(SE\) cùng nằm trong mặt phẳng \(\left( {SIB} \right)\), nên giao điểm của \(IJ\) và \(SE\) chính là giao điểm giữa \(IJ\) và mặt phẳng \(\left( {SAC} \right)\).
Vậy \(K\) là giao điểm giữa \(IJ\) và \(SE\).
b) Gọi giao điểm giữa \(AC\) và \(BD\) là \(F\).
Trong mặt phẳng \(\left( {SBD} \right)\) lấy \(DJ\) giao với \(SF\) tại \(L\).
Vì \(SF\) nằm trên \(\left( {SAC} \right)\) nên \(L\) là giao điểm giữa \(DJ\) và mặt phẳng \(\left( {SAC} \right)\).
c) \(K \in IJ \Rightarrow K \in \left( {OAJ} \right)\), mà \(K \in \left( {SAC} \right)\) nên \(K\) là điểm chung giữa 2 mặt phẳng \(\left( {OAJ} \right)\) và mặt phẳng \(\left( {SAC} \right) \Rightarrow \)\(K\) thuộc giao tuyến giữa 2 mặt phẳng này (1).
Tương tự, \(L \in JD \Rightarrow L \in \left( {OAJ} \right)\), mà \(L \in \left( {SAC} \right)\) nên \(L\) thuộc giao tuyến giữa mặt phẳng \(\left( {OAJ} \right)\) và mặt phẳng \(\left( {SAC} \right)\) (2).
Mặt khác, \(M \in OJ \Rightarrow M \in \left( {OAJ} \right)\), mà \(M \in SC \Rightarrow M \in \left( {SAC} \right) \Rightarrow M\) là điểm chung giữa mặt phẳng \(\left( {OAJ} \right)\) và mặt phẳng \(\left( {SAC} \right)\), kết hợp \(A\) là điểm chung giữa mặt phẳng \(\left( {OAJ} \right)\) và mặt phẳng \(\left( {SAC} \right) \Rightarrow AM\) là giao tuyến giữa mặt phẳng \(\left( {OAJ} \right)\) và mặt phẳng \(\left( {SAC} \right)\) (3).
Từ (1), (2) và (3) suy ra \(A,K,L,M\) thẳng hàng. (đpcm)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
