Trong các câu sau đây, câu nào là đúng?

A. \(\frac{{ - 4}}{5} < \frac{{ - 1}}{3} < 0 < 4 < 2,25\)

B. \(\frac{{ - 1}}{3} < \frac{{ - 4}}{5} < 0 < 2,25 < 4\)

C. \[0 < \frac{{ - 1}}{3} < \frac{{ - 4}}{5} < 2,25 < 4\]

D. \(\frac{{ - 4}}{5} < \frac{{ - 1}}{3} < 0 < 2,25 < 4\).

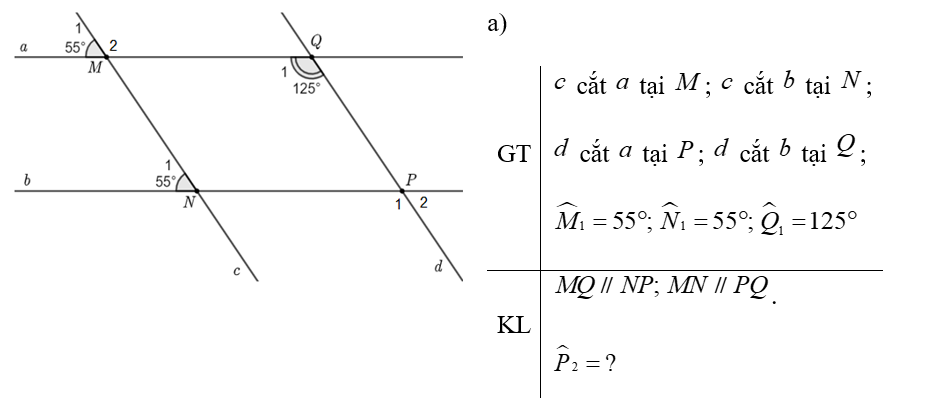
b) Ta thấy \({\widehat M_1} = {\widehat N_1} = 55^\circ \) mà \({\widehat M_1}\) và \({\widehat N_1}\) ở vị trí đồng vị.

Do đó \[MQ\parallel NP\].

Vì \({\widehat M_1}\) và \({\widehat M_2}\) là hai góc kề bù nên \({\widehat M_1} + {\widehat M_2} = 180^\circ \).

Suy ra \({\widehat M_2} = 180^\circ - {\widehat M_1} = 180^\circ - 55^\circ = 125^\circ \).

Ta thấy \({\widehat M_2} = {\widehat Q_1} = 125^\circ \) mà \({\widehat M_2}\) và \({\widehat Q_1}\) ở vị trí so le trong.

Do đó \[MN\parallel PQ\].

Vậy \[MQ\parallel NP & ;\,\,MN\parallel PQ\].

c) Vì \[MQ\parallel NP\] nên \[{\widehat P_1} = {\widehat Q_1} = 125^\circ \] (hai góc đồng vị)

Vì \({\widehat P_1}\) và \({\widehat P_2}\) là hai góc kề bù nên \[{\widehat P_1} + {\widehat P_2} = 180^\circ \].

Suy ra \[{\widehat P_2} = 180^\circ - {\widehat P_1} = 180^\circ - 125^\circ = 55^\circ \].

Vậy \[{\widehat P_2} = 55^\circ \].

Ta có: \(2022A = \frac{{2022\left( {1 + {{2022}^{2022}}} \right)}}{{1 + {{2022}^{2023}}}} = \frac{{2022 + {{2022}^{2023}}}}{{1 + {{2022}^{2023}}}} = 1 + \frac{{2021}}{{1 + {{2022}^{2023}}}}\);

\(2022B = \frac{{2022\left( {1 + {{2022}^{2023}}} \right)}}{{1 + {{2022}^{2024}}}} = \frac{{2022 + {{2022}^{2024}}}}{{1 + {{2022}^{2024}}}} = 1 + \frac{{2021}}{{1 + {{2022}^{2024}}}}\).

Vì \(\frac{1}{{1 + {{2022}^{2023}}}} > \frac{1}{{1 + {{2022}^{2024}}}}\) nên \(\frac{{2021}}{{1 + {{2022}^{2023}}}} > \frac{{2021}}{{1 + {{2022}^{2024}}}}\)

Suy ra \(1 + \frac{{2021}}{{1 + {{2022}^{2023}}}} > 1 + \frac{{2021}}{{1 + {{2022}^{2024}}}}\) hay \(2022A < 2022B\).

Vậy \(A < B\).