(1,0 điểm) Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 10 cm và chiều rộng là 6 cm. Hỏi độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu centimet (làm tròn kết quả đến hàng phần trăm)?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Độ dài đường chéo của hình chữ nhật là:
\(\sqrt {{{10}^2} + {6^2}} = \sqrt {136} \approx 11,66\) (cm)
Vậy độ dài đường chéo của hình chữ nhật đó xấp xỉ 11,66 cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \(2022A = \frac{{2022\left( {1 + {{2022}^{2022}}} \right)}}{{1 + {{2022}^{2023}}}} = \frac{{2022 + {{2022}^{2023}}}}{{1 + {{2022}^{2023}}}} = 1 + \frac{{2021}}{{1 + {{2022}^{2023}}}}\);
\(2022B = \frac{{2022\left( {1 + {{2022}^{2023}}} \right)}}{{1 + {{2022}^{2024}}}} = \frac{{2022 + {{2022}^{2024}}}}{{1 + {{2022}^{2024}}}} = 1 + \frac{{2021}}{{1 + {{2022}^{2024}}}}\).
Vì \(\frac{1}{{1 + {{2022}^{2023}}}} > \frac{1}{{1 + {{2022}^{2024}}}}\) nên \(\frac{{2021}}{{1 + {{2022}^{2023}}}} > \frac{{2021}}{{1 + {{2022}^{2024}}}}\)
Suy ra \(1 + \frac{{2021}}{{1 + {{2022}^{2023}}}} > 1 + \frac{{2021}}{{1 + {{2022}^{2024}}}}\) hay \(2022A < 2022B\).
Vậy \(A < B\).
Lời giải
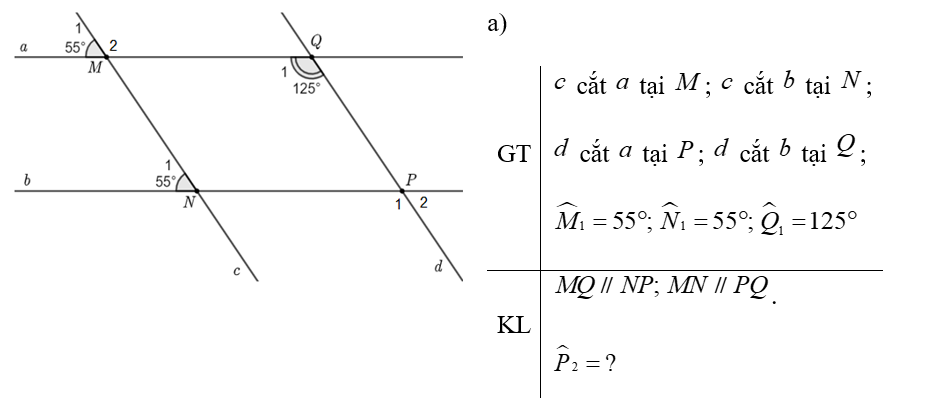
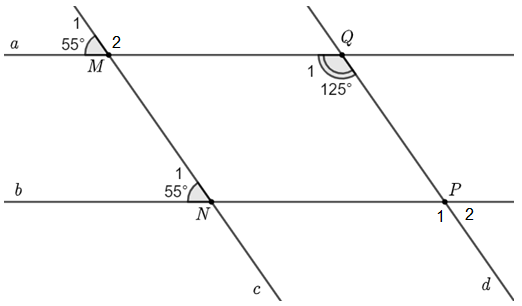
b) Ta thấy \({\widehat M_1} = {\widehat N_1} = 55^\circ \) mà \({\widehat M_1}\) và \({\widehat N_1}\) ở vị trí đồng vị.
Do đó \[MQ\parallel NP\].
Vì \({\widehat M_1}\) và \({\widehat M_2}\) là hai góc kề bù nên \({\widehat M_1} + {\widehat M_2} = 180^\circ \).
Suy ra \({\widehat M_2} = 180^\circ - {\widehat M_1} = 180^\circ - 55^\circ = 125^\circ \).
Ta thấy \({\widehat M_2} = {\widehat Q_1} = 125^\circ \) mà \({\widehat M_2}\) và \({\widehat Q_1}\) ở vị trí so le trong.
Do đó \[MN\parallel PQ\].
Vậy \[MQ\parallel NP & ;\,\,MN\parallel PQ\].
c) Vì \[MQ\parallel NP\] nên \[{\widehat P_1} = {\widehat Q_1} = 125^\circ \] (hai góc đồng vị)
Vì \({\widehat P_1}\) và \({\widehat P_2}\) là hai góc kề bù nên \[{\widehat P_1} + {\widehat P_2} = 180^\circ \].
Suy ra \[{\widehat P_2} = 180^\circ - {\widehat P_1} = 180^\circ - 125^\circ = 55^\circ \].
Vậy \[{\widehat P_2} = 55^\circ \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
1,3(45)
\(\sqrt 3 \)
\(\frac{{ - 5}}{4}\)
\(\frac{{10}}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
120°
60°
50°
Không xác định được.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.