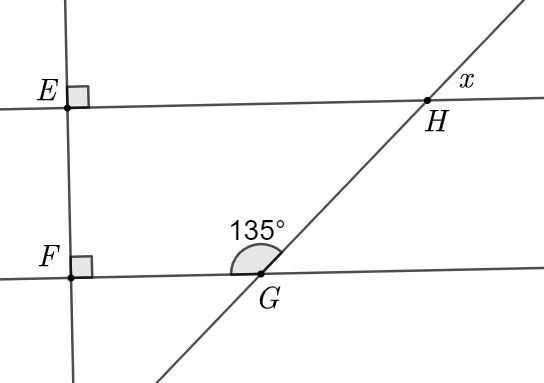
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: B
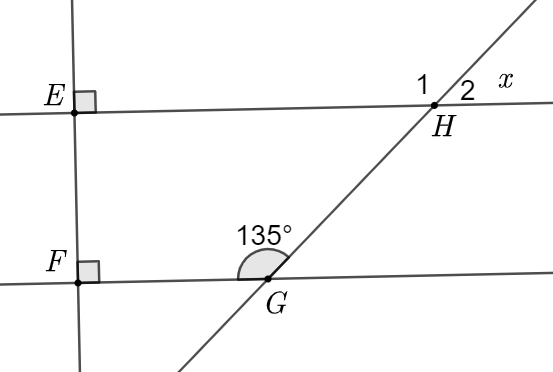
Đặt \[{\widehat H_1};\,\,{\widehat H_2}\] như hình vẽ.
Quan sát hình vẽ trên, ta có \(EF \bot EH;\,\,EF \bot FG\) nên \(EH\parallel FG\).
Suy ra \(\widehat {FGH} = {\widehat H_1}\) (hai góc đồng vị).
Vì \[{\widehat H_1}\] và \[{\widehat H_2}\] là hai góc kề bù nên \[{\widehat H_1} + {\widehat H_2} = 180^\circ \].
Do đó \[{\widehat H_2} = 180^\circ - {\widehat H_1} = 180^\circ - 135^\circ = 45^\circ \].
Vậy \[x = 45^\circ \].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

b) Theo giả thiết \(a\parallel b\); \(AB \bot b\) tại \(B\) nên \(AB \bot a\) tại \(A\) hay \(\widehat {BAE} = 90^\circ \).
Vì \(a\parallel b\) nên \[\widehat {AED} = {\widehat D_1} = 65^\circ \] (hai góc so le trong).
Vì \(\widehat {BDE}\) và \[{\widehat D_1}\] là hai góc kề bù nên \(\widehat {BDE} + {\widehat D_1} = 180^\circ \).
Suy ra \[\widehat {BDE} + {\widehat D_1} = 180^\circ - 65^\circ = 115^\circ \].
Vậy \(\widehat {BAE} = 90^\circ \) và \(\widehat {BDE} = 115^\circ \).
Lời giải
Khi bán 80 cái áo với giá mỗi cái áo lãi 20% so với giá gốc thì số tiền lãi thu được là:
\(200\,\,000\,\,.\,\,80\,\,.\,\,20\% = 3\,\,200\,\,000\) (đồng).
Khi bán 20 cái áo còn lại mỗi cái bán lỗ 10% so với giá gốc thì số tiền bị lỗ là:
\(200\,\,000\,\,.\,\,20\,\,.\,\,10\% = 400\,\,000\) (đồng).
Vì số tiền lãi khi bán 80 cái áo nhiều hơn số tiền bị lỗ khi bán 20 cái áo còn lại nên sau khi bán hết 100 cái áo cửa hàng đó lãi số tiền là:
\[3\,\,200\,\,000 - 400\,\,000 = 2\,\,800\,\,000\] (đồng).
Vậy sau khi bán hết 100 cái áo cửa hàng đó lãi 2 800 000 đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\[\frac{{ - 1}}{{\sqrt {15} }}\]
\[\frac{1}{{\sqrt {15} }}\]
\[\frac{1}{{ - \sqrt {15} }}\]
\[\sqrt {15} \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.