(a) Hãy biểu diễn các số hữu tỉ sau dưới dạng số thập phân: \[\frac{{22}}{5};\,\,\frac{{16}}{3};\,\,\,\frac{{47}}{2};\,\,\frac{{35}}{{12}}\].
(b) Tính: \(\sqrt {{{12}^2}} ;\,\,\sqrt {64} ;\,\,\sqrt {{{\left( { - 14} \right)}^2}} \).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có \[\frac{{22}}{5} = 4,4;\,\,\frac{{16}}{3} = 5,333... = 5,(3);\,\,\,\frac{{47}}{2} = 23,5;\,\,\frac{{35}}{{12}} = 2,9166.. = 2,91(6)\].
Vậy các số hữu tỉ \[\frac{{22}}{5};\,\,\frac{{16}}{3};\,\,\,\frac{{47}}{2};\,\,\frac{{35}}{{12}}\] được biểu diễn dưới dạng số thập phân lần lượt là
\[4,4;\,\,5,(3);\,\,\,23,5;\,\,2,91(6)\].
b) Ta có: \(\sqrt {{{12}^2}} = 12;\,\,\sqrt {64} = \sqrt {{8^2}} = 8;\,\,\sqrt {{{\left( { - 14} \right)}^2}} = \sqrt {{{14}^2}} = 14\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Có 2 đường chéo
Có 6 mặt, 8 cạnh và 12 đỉnh
Lời giải
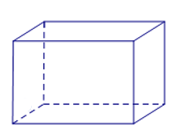
Đáp án đúng là: B
Hình hộp chữ nhật có:
• 6 mặt, 8 cạnh và 12 đỉnh;
• 4 đường chéo;
• các mặt bên là các hình chữ nhật không bằng nhau.
• các cạnh bên bằng nhau, các cạnh đáy không bằng nhau.
Vậy ta chọn phương án B.
Câu 2
Song song và không bằng nhau
Cắt nhau
Vuông góc với nhau
Song song và bằng nhau.
Lời giải
Đáp án đúng là: D
Các cạnh bên của hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác song song và bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\(\frac{{ - 4}}{5}\)
\(1,2\)
\(\frac{{14}}{0}\)
\(1\frac{2}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập