(2,5 điểm)
(a) Cho hình lăng trụ đứng có đáy là hình thang cân với các kích thước như hình vẽ. Tính diện tích xung quanh và thể tích của hình lăng trụ đó.
(b) Một căn phòng có chiều dài \(4,5\,\,{\rm{m}}\), chiều rộng \(4\,\,{\rm{m}}\) và chiều cao \[3,5\,\,{\rm{m}}\].
(i) Tính diện tích xung quanh và thể tích khoảng không gian bên trong căn phòng.
(ii) Người ta dự định dùng giấy dán tường dán kín bốn bức tường của căn phòng. Mỗi tờ giấy dán tường có diện tích \(16,5\,\,{m^2}\). Coi các mạch ghép là không đáng kể, hỏi người ta cần mua ít nhất bao nhiêu tờ giấy dán tường? (Biết rằng diện tích cửa phòng là \(\left. {1,2\,\,{m^2}} \right)\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:


Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số tiền chị Hương trả góp trong vòng một năm (12 tháng) là:
\(700.12 = 8\,\,400\) (nghìn đồng) = 8,4 (triệu đồng).
Số tiền trả góp này ứng với \(100\% - 40\% = 60\% \) (tổng số tiền).
Chị Hương đã mua chiếc điện thoại với số tiền là: \(8,4:60\% = 14\) (triệu đồng).
Vậy chị Hương đã mua chiếc điện thoại với số tiền là 14 triệu đồng.
Lời giải
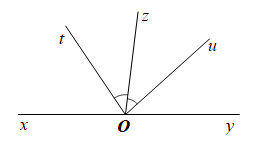
a) Học sinh vẽ hình đúng số đo góc.
Các cặp góc kề bù có trong hình vẽ là: \(\widehat {xOt}\) và \(\widehat {tOy}\); \(\widehat {xOz}\) và \(\widehat {zOy}\); \(\widehat {xOu}\) và \(\widehat {uOy}\).
b) Tính số đo của góc \(\widehat {tOz},\,\,\widehat {tOy}\).
Ta có tia \(Oz\) là tia phân giác của góc \(tOu\) nên: \(\widehat {tOz} = \frac{1}{2}\widehat {tOu} = 41^\circ \).
Ta có \(\widehat {tOx} + \widehat {tOz} = \widehat {xOz}\)
Nên \(\widehat {tOx} = \widehat {xOz} - \widehat {tOz} = 97^\circ - 41^\circ = 56^\circ \).
Do \(\widehat {tOx} + \widehat {tOy} = 180^\circ \)
Suy ra \(\widehat {tOy} = 180^\circ - \widehat {tOx} = 180^\circ - 56^\circ = 124^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\( - \frac{3}{2};\,\,\frac{0}{7};\,\,\frac{7}{0};\,\,\frac{{ - 2}}{{ - 5}}\)
\(1\frac{2}{7};\,\,\frac{0}{7};\,\,\frac{7}{0};\,\,\frac{{ - 2}}{{ - 5}}\)
\( - \frac{3}{2};\,\,1\frac{2}{7};\,\,\frac{7}{0};\,\,\frac{{ - 2}}{{ - 5}}\)
\( - \frac{3}{2};\,\,1\frac{2}{7};\,\,\frac{0}{7};\,\,\frac{{ - 2}}{{ - 5}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.