1. Một cái bể cá có chiều dài 2 m; chiều rộng 80 cm và chiều cao 80 cm. Người ta cần đổ vào bể cá bao nhiêu m³ nước thì đầy bể?

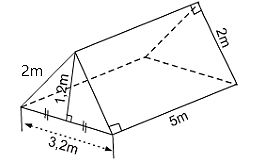
2. Một nhóm học sinh cần chuẩn bị lều để đi cắm trại. Nhóm dự tính dựng lều trại hình lăng trụ đứng tam giác với kích thức như hình vẽ. Lều được phủ kín bằng vải bạt (tính cả mặt tiếp xúc với mặt đất) có giá 150 000 đồng / m². Số tiền tối đa chi cho mua vải là 6 000 000 đồng. Hỏi nhóm học sinh có đủ tiền mua vải không?

1.

a) \(A = 3:{\left( {\frac{{ - 3}}{2}} \right)^2} + \frac{1}{9}\,\,.\,\sqrt {36} + 0,75\)\( = 3:\frac{9}{4} + \frac{1}{9}.6 + 0,75\)

\( = 3\,\,.\,\,\frac{4}{9} + \frac{2}{3} + 0,75\)\(A = \frac{4}{3} + \frac{2}{3} + 0,75\)\( = 2 + 0,75\)\( = 2,75\).

b) \(B = \left( {8 - \frac{2}{3} + \frac{1}{2}} \right) - \left( {5 - \frac{7}{3} - \frac{3}{2}} \right) - \left( {\frac{5}{3} + \frac{5}{2} + 4} \right)\).

\[ = 8 - \frac{2}{3} + \frac{1}{2} - 5 + \frac{7}{3} + \frac{3}{2} - \frac{5}{3} - \frac{5}{2} - 4\]

\[ = \left( {8 - 5 - 4} \right) + \left( { - \frac{2}{3} + \frac{7}{3} - \frac{5}{3}} \right) + \left( {\frac{1}{2} + \frac{3}{2} - \frac{5}{2}} \right)\]

\[ = - 1 + 0 + \frac{{ - 1}}{2}\]\[ = \frac{{ - 3}}{2}\].

2.

a) \(\frac{3}{4} - \left( {x + \frac{1}{2}} \right) = \frac{1}{4}\)

\(x + \frac{1}{2} = \frac{3}{4} - \frac{1}{4}\)

\(x + \frac{1}{2} = \frac{1}{2}\)

\(x = \frac{1}{2} - \frac{1}{2}\)

\(x = 0\)

Vậy \(x = 0\).

b) \({\left( {x - \frac{2}{3}} \right)^2} + \frac{{16}}{{25}} = 1\)

\[{\left( {x - \frac{2}{3}} \right)^2} = 1 - \frac{{16}}{{25}}\]

\[{\left( {x - \frac{2}{3}} \right)^2} = \frac{9}{{25}}\]

\[{\left( {x - \frac{2}{3}} \right)^2} = {\left( {\frac{3}{5}} \right)^2} = {\left( {\frac{{ - 3}}{5}} \right)^2}\]

TH1: \(x - \frac{2}{3} = \frac{3}{5}\)

\(x = \frac{3}{5} + \frac{2}{3}\)

\(x = \frac{{19}}{{15}}\)

TH2: \(x - \frac{2}{3} = \frac{{ - 3}}{5}\)

\(x = \frac{{ - 3}}{5} + \frac{2}{3}\)

\(x = \frac{1}{{15}}\)

Vậy \[x \in \left\{ {\frac{{19}}{{15}};\,\,\frac{1}{{15}}} \right\}\].

Mỗi chiếc ti vi lãi số tiền là:

\(6{\rm{ }}400{\rm{ }}000\,\,.\,\,20\% = 1{\rm{ }}280{\rm{ }}000\) (đồng)

Nếu bán hết 20 chiếc ti vi thì số tiền lãi là:

\(20\,\,.\,\,1{\rm{ 280 000 = 25 600 000}}\) (đồng).

Vậy nếu bán hết 20 chiếc ti vi thì số tiền lãi là 25 600 000 đồng.