a) Cho tứ giác \(ABCD\), biết rằng \[\frac{{\widehat {A\,\,}}}{1} = \frac{{\widehat {B\,}}}{2} = \frac{{\widehat {C\,}}}{3} = \frac{{\widehat {D\,}}}{4}.\] Tính \(\widehat {B\,}.\)

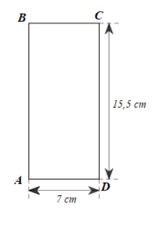
b) Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết 1 inch \( \approx 2,54\;\,\,{\rm{cm}}{\rm{,}}\) điện thoại có chiều rộng là \(7\,\,\;{\rm{cm;}}\) chiều dài là \(15,5\,\,{\rm{cm}}{\rm{.}}\) Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch? (Làm tròn kết quả đến hàng đơn vị)

a) Đường cao mặt bên hình chóp chính là trung đoạn \[d = 67,5\;\;{\rm{mm}}\]

Diện tích xung quanh của khối rubik đó là:

\({S_{xq}} = \frac{1}{2} \cdot C \cdot d = \frac{1}{2} \cdot 234 \cdot 67,5 = 7\,\,897,5\;\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)

Đáy là tam giác đều có cạnh là \[234:3 = 78\;\;{\rm{cm}}\];

Chiều cao của tam giác đáy là \[67,5\;\;{\rm{cm}}\].

Diện tích mặt đáy của khối rubik đó là: \(\frac{1}{2} \cdot 78 \cdot 67,5 = 2\,\,632,5\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

Diện tích toàn phần của khối rubik đó là: \({S_{tp}} = 7\,\,897,5 + 2\,632,5 = 10\,\,530\,\,\;\;\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

b) Thể tích của khối rubik đó là: \(V = \frac{1}{3} \cdot 2\,\,632,5 \cdot 63,7 = 55\,\,896,75\;\;\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)

A = \frac{4}{{{x^2} + x + 1}}\) và \(B = \frac{2}{{1 - x}} + \frac{{2{x^2} + 4x}}{{{x^3} - 1}}\) với \(x \ne 1.\)

a) Thay \(x =  - 2\) (thỏa mãn) vào biểu thức \(A\) ta được:

\[A = \frac{4}{{{{\left( { - 2} \right)}^2} + \left( { - 2} \right) + 1}} = \frac{4}{{4 - 2 + 1}} = \frac{4}{3}.\]

b) Ta có \(A = B + C\) nên \(C = A - B\)

\(C = \frac{4}{{{x^2} + x + 1}} - \left( {\frac{2}{{1 - x}} + \frac{{2{x^2} + 4x}}{{{x^3} - 1}}} \right)\)

\( = \frac{4}{{{x^2} + x + 1}} - \frac{2}{{1 - x}} - \frac{{2{x^2} + 4x}}{{{x^3} - 1}}\)

\( = \frac{4}{{{x^2} + x + 1}} + \frac{2}{{x - 1}} - \frac{{2{x^2} + 4x}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)

\( = \frac{{4\left( {x - 1} \right) + 2\left( {{x^2} + x + 1} \right) - \left( {2{x^2} + 4x} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)

\( = \frac{{4x - 4 + 2{x^2} + 2x + 2 - 2{x^2} - 4x}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)

\( = \frac{{2x - 2}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)

\( = \frac{{2\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)\( = \frac{2}{{{x^2} + x + 1}}\)

Vậy với \(x \ne 1\) ta có \(C = \frac{2}{{{x^2} + x + 1}}.\)

c) Với \(x \ne 1\) ta có \[C = \frac{2}{{{x^2} + x + 1}} = \frac{2}{{{x^2} + 2 \cdot x \cdot \frac{1}{2} + \frac{1}{4} + \frac{3}{4}}} = \frac{2}{{{{\left( {x + \frac{1}{2}} \right)}^2} + \frac{3}{4}}}\]

Mà \({\left( {x + \frac{1}{2}} \right)^2} \ge 0\) nên \({\left( {x + \frac{1}{2}} \right)^2} + \frac{3}{4} > 0\), do đó \[C = \frac{2}{{{{\left( {x + \frac{1}{2}} \right)}^2} + \frac{3}{4}}} > 0\] với mọi \(x \ne 1.\)