Một phòng học có nền nhà hình chữ nhật với chiều rộng là \(5\,\,{\rm{m}}\) và chiều dài hơn chiều rộng \(3\,\,{\rm{m}}\).
a) Tính diện tích nền phòng học đó.
b) Để lát nền phòng học trên, người ta dùng loại gạch men hình vuông có cạnh là \[40\,\,{\rm{cm}}{\rm{.}}\] Nếu một viên gạch giá \[24{\rm{ }}000\] đồng và tiền công lát nền trả cho \(1\,\,{{\rm{m}}^2}\) là \[50{\rm{ }}000\] đồng thì tổng số tiền phải trả cho việc lát nền căn phòng là bao nhiêu? bỏ qua những mép vữa không đáng kể.
Một phòng học có nền nhà hình chữ nhật với chiều rộng là \(5\,\,{\rm{m}}\) và chiều dài hơn chiều rộng \(3\,\,{\rm{m}}\).
a) Tính diện tích nền phòng học đó.
b) Để lát nền phòng học trên, người ta dùng loại gạch men hình vuông có cạnh là \[40\,\,{\rm{cm}}{\rm{.}}\] Nếu một viên gạch giá \[24{\rm{ }}000\] đồng và tiền công lát nền trả cho \(1\,\,{{\rm{m}}^2}\) là \[50{\rm{ }}000\] đồng thì tổng số tiền phải trả cho việc lát nền căn phòng là bao nhiêu? bỏ qua những mép vữa không đáng kể.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 6 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
a) Chiều dài của hình nền nhà hình chữ nhật đó là: 5 + 3 = 8 (m)
Diện tích nền phòng học đó là: \[5.8 = 40\,\,\left( {{{\rm{m}}^2}} \right)\].
b) Diện tích một viên gạch men hình vuông cạnh \(40\,\,{\rm{cm}}\) là:
\({40.40} = 1600\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right) = 0,16\,\,\left( {{{\rm{m}}^2}} \right)\).
Số viên gạch cần dùng để lát nền căn phòng là:
\(40:0,16 = 250\) (viên).
Do đó cần 250 viên gạch để lát nền phòng học.
Số tiền mua gạch men là:
\(24 000.250 = 6 000 000\) (đồng).
Số tiền công lát nền là:
\(50{\rm{ }}000 .40 = 2 000{\rm{ }}000\) (đồng).
Vậy tổng số tiền phải trả để lát nền căn phòng học đó là:
\[6 000 000 + 2 000 000 = 8 000 000\] (đồng).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: C
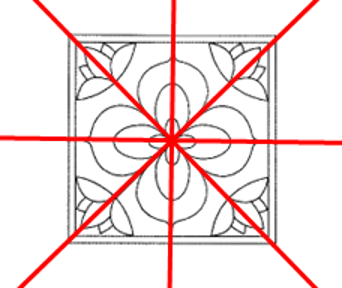
Hình vẽ đã cho có 4 trục đối xứng như sau:
Câu 2
Lời giải
Đáp án đúng là: B
Trong hình tam giác đều, mỗi góc bằng \(60^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[\left\{ {1;2;3;4;6;12} \right\}\];
B. \(\left\{ { - 1; - 2; - 3; - 4; - 5; - 6; - 12} \right\}\);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Cộng tiền 3 lần;
B. Cộng tiền 2 lần và trừ tiền 1 lần;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Chu vi của hình vuông là \(20\,\,{\rm{c}}{{\rm{m}}^2}\);
B. Các cạnh \[AB\] và \[AD\] song song;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.