Cho hai đơn thức \(M = {\left( {3{a^2}b} \right)^3}{\left( {a{b^3}} \right)^2};\) \(N = {\left( {{a^2}b} \right)^4}.\) Kết quả của phép chia \(M:N\) là
Câu hỏi trong đề: Bộ 10 đề thi Cuối kì 1 Toán 8 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
Ta có \(M = {\left( {3{a^2}b} \right)^3}{\left( {a{b^3}} \right)^2} = 27{a^6}{b^3} \cdot {a^2}{b^6} = 27{a^8}{b^9}.\)
\(N = {\left( {{a^2}b} \right)^4} = {a^8}{b^4}.\)
Khi đó \[M:N = \left( {27{a^8}{b^9}} \right):\left( {{a^8}{b^4}} \right) = \left( {27:1} \right) \cdot \left( {{a^8}:{a^8}} \right) \cdot \left( {{b^9}:{b^4}} \right) = 27{b^5}.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
1)

a) Xét \(\Delta ABC\) cân tại \(A\) có \(AH\) là đường trung tuyến nên đồng thời là đường cao của tam giác.
Do đó \(AH \bot BC\) nên \(\Delta AHB\) và \(\Delta AHC\) đều vuông tại \(H.\)
Xét \(\Delta AHB\) vuông tại \(H\) có \(HK\) là đường trung tuyến ứng với cạnh huyền \(AB\) nên \(KH = \frac{1}{2}AB\) (tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông).
Tương tự, xét \(\Delta AHC\) vuông tại \(H\) ta có \(IH = \frac{1}{2}AC.\)
Mà \(I,\) \(K\) lần lượt là trung điểm của \(AC\) và \(AB\) nên \(KA = KB = \frac{1}{2}AB;\) \(IA = IC = \frac{1}{2}AC.\)
Lại có \(AB = AC\) (do \(\Delta ABC\) cân tại \(A)\)
Do đó \(KA = KH = IA = IH.\)
Xét tứ giác \(AKHI\) có \(KA = KH = IA = IH\) nên là hình thoi.
b) Xét tứ giác \(AHCE\) có \(I\) là trung điểm của hai đường chéo \(AC,HE\) nên \(AHCE\) là hình bình hành.
Lại có \(\widehat {AHC} = 90^\circ \) nên hình bình hành \(AHCE\) là hình chữ nhật.
Để hình chữ nhật \(AHCE\) là hình vuông thì hai cạnh kề bằng nhau, tức \(HA = HC.\)
Mà \(H\) là trung điểm của \(BC\) nên \(HB = HC = \frac{1}{2}BC.\)
Khi đó \[HA = HB = HC = \frac{1}{2}BC.\]
Xét \(\Delta ABC\) có đường trung tuyến \(AH\) thỏa mãn \[HA = \frac{1}{2}BC\] nên \(\Delta ABC\) vuông tại \(A.\)
Vậy \(\Delta ABC\) vuông cân tại \(A\) thì \(AHCE\) là hình vuông.
2)

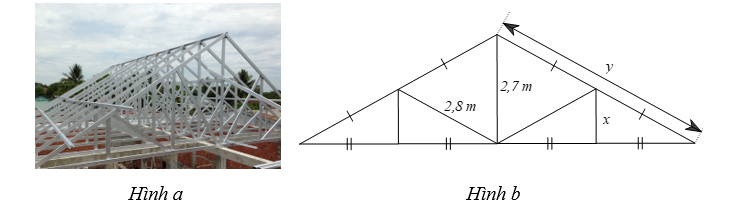
Đặt các điểm \[A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D,{\rm{ }}E,{\rm{ }}M,{\rm{ }}N,{\rm{ }}P\] như hình vẽ trên.
⦁ Xét \(\Delta AMC\) có \(E,P\) lần lượt là trung điểm của \(AC,MC\) (do \(EA = EC,PM = PC)\) nên \(EP\) là đường trung bình của \(\Delta AMC.\)
Do đó \(EP = \frac{1}{2}AM = \frac{1}{2} \cdot 2,7 = 1,35{\rm{\;}}\left( {\rm{m}} \right)\) (tính chất đường trung bình của tam giác).
Hay \(x = 1,35{\rm{\;}}\left( {\rm{m}} \right){\rm{.}}\)
⦁ Ta có \(MB = MN + NB\) và \(MC = MP + PC\)
Mà \(MN = NB = MP = PC\) nên \(MB = MC.\)
Xét \(\Delta ABC\) có \(D,M\) lần lượt là trung điểm của \(AB,BC\) (do \(DB = DA,MB = MC)\) nên \(DM\) là đường trung bình của \(\Delta ABC.\)
Do đó \[DM = \frac{1}{2}AC\] (tính chất đường trung bình của tam giác).
Suy ra \(AC = 2DM = 2 \cdot 2,8 = 5,6{\rm{\;}}\left( {\rm{m}} \right).\) Hay \[y = 5,6{\rm{\;}}\left( {\rm{m}} \right).\]
Vậy độ dài của cây chống đứng bên và độ dài của của cánh kèo lần lượt là \(x = 1,35{\rm{\;}}\left( {\rm{m}} \right);\) \(y = 5,6{\rm{\;}}\left( {\rm{m}} \right).\)
Lời giải
Hướng dẫn giải
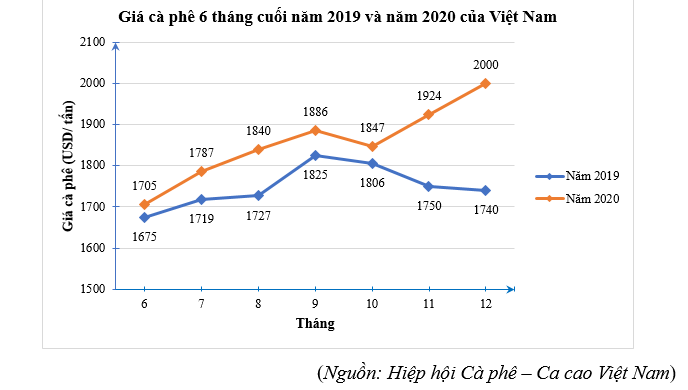
a) Biểu đồ đã cho là biểu đồ đoạn thẳng.
Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập gián tiếp bằng cách truy cập website của Hiệp hội Cà phê – Ca cao Việt Nam.
b) Bảng thống kê tương ứng cho dữ liệu trong biểu đồ đã cho:
|
Giá cà phê 6 tháng cuối năm 2019 và năm 2020 của Việt Nam (USD/ tấn) |
|||||||
|
Tháng Năm |
Tháng 6 |
Tháng 7 |
Tháng 8 |
Tháng 9 |
Tháng 10 |
Tháng 11 |
Tháng 12 |
|
Năm 2019 |
1675 |
1719 |
1727 |
1825 |
1806 |
1750 |
1740 |
|
Năm 2020 |
1705 |
1787 |
1840 |
1886 |
1847 |
1924 |
2000 |
Nếu chọn một biểu đồ khác để biểu diễn dữ liệu trên, ta nên chọn loại biểu đồ cột kép.
c) Ta có bảng thống kê bổ sung sự tăng giá mỗi tấn cà phê của năm 2020 so với năm 2019 như sau:
|
Giá cà phê 6 tháng cuối năm 2019 và năm 2020 của Việt Nam (USD/ tấn) |
||||||||
|
Tháng Năm |
Tháng 6 |
Tháng 7 |
Tháng 8 |
Tháng 9 |
Tháng 10 |
Tháng 11 |
Tháng 12 |
|
|
Năm 2019 |
1675 |
1719 |
1727 |
1825 |
1806 |
1750 |
1740 |
|
|
Năm 2020 |
1705 |
1787 |
1840 |
1886 |
1847 |
1924 |
2000 |
|
|
Sự tăng giá cà phê mỗi tấn |
30 |
68 |
113 |
61 |
41 |
174 |
260 |
|
Vậy, trong sáu tháng cuối năm 2020, tháng 12 có sự tăng giá cà phê mạnh nhất so với cùng kì năm trước.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.