(0,5 điểm) Cho \({a^3} + {b^3} + {c^3} = 3abc\) và \(a + b + c \ne 0.\) Tính giá trị của biểu thức:
\(N = \frac{{{a^2} + {b^2} + {c^2}}}{{{{\left( {a + b + c} \right)}^2}}}.\)
(0,5 điểm) Cho \({a^3} + {b^3} + {c^3} = 3abc\) và \(a + b + c \ne 0.\) Tính giá trị của biểu thức:
\(N = \frac{{{a^2} + {b^2} + {c^2}}}{{{{\left( {a + b + c} \right)}^2}}}.\)
Câu hỏi trong đề: Bộ 10 đề thi Cuối kì 1 Toán 8 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Ta có:
\({a^3} + {b^3} + {c^3} = 3abc\)
\({a^3} + {b^3} + {c^3} - 3abc = 0\)
\({\left( {a + b} \right)^3} - 3ab\left( {a + b} \right) + {c^3} - 3abc = 0\)
\({\left( {a + b} \right)^3} + {c^3} - 3ab\left( {a + b + c} \right) = 0\)
\({\left( {a + b + c} \right)^3} - 3\left( {a + b} \right)c\left( {a + b + c} \right) - 3ab\left( {a + b + c} \right) = 0\)
\(\left( {a + b + c} \right)\left[ {{{\left( {a + b + c} \right)}^2} - 3ac - 3bc - 3ab} \right] = 0\)
\(\left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ac - bc - ab} \right) = 0\)
Suy ra \({a^2} + {b^2} + {c^2} - ac - bc - ab = 0\) (do \(a + b + c \ne 0).\)
Nên \[{a^2} + {b^2} + {c^2} = ab + bc + ca.\]
Khi đó ta có \(N = \frac{{{a^2} + {b^2} + {c^2}}}{{{{\left( {a + b + c} \right)}^2}}} = \frac{{{a^2} + {b^2} + {c^2}}}{{{a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right)}}\)
\( = \frac{{{a^2} + {b^2} + {c^2}}}{{{a^2} + {b^2} + {c^2} + 2\left( {{a^2} + {b^2} + {c^2}} \right)}} = \frac{{{a^2} + {b^2} + {c^2}}}{{3\left( {{a^2} + {b^2} + {c^2}} \right)}} = \frac{1}{3}.\)
Vậy \(N = \frac{1}{3}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
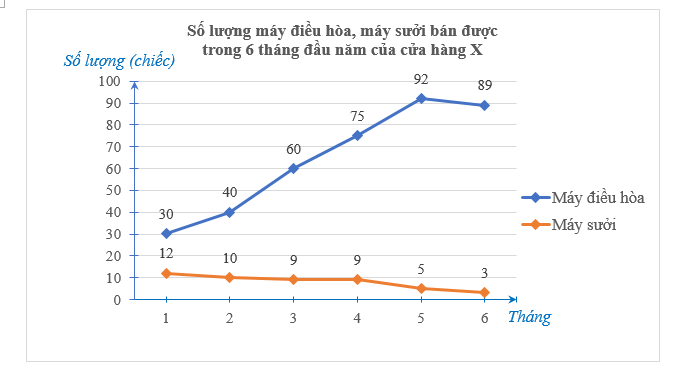
a) Biểu đồ trên là biểu đồ đoạn thẳng. Do số lượng máy bán được mỗi loại được nhân viên cửa hàng báo cáo hàng tháng qua văn bản nên để thu thập được dữ liệu thì quản lí cửa hàng chỉ cần thu thập từ văn bản báo cáo có sẵn nhận được từ nhân viên. Do đó phương pháp thu thập này là gián tiếp.
b) Số máy điều hòa mà cửa hàng X bán được trong 6 tháng đầu năm là:
\(30 + 40 + 60 + 75 + 92 + 89 = 386\) (chiếc).
Số máy sưởi mà cửa hàng X bán được trong 6 tháng đầu năm là:
\(12 + 10 + 9 + 9 + 5 + 3 = 48\) (chiếc).
Do đó, trong 6 tháng đầu năm, cửa hàng X bán được số máy điều hòa nhiều hơn số máy sưởi là: \(386 - 48 = 338\) (chiếc).
c) Vì tổng số máy sưởi bán được trong hai tháng 5 và 6 là: \(5 + 3 = 8\) (chiếc) \( < 9\) chiếc nên cửa hàng sẽ ngừng kinh doanh máy sưởi sau 6 tháng kinh doanh.
Lời giải
Hướng dẫn giải
|
a) \({\left( {x - 2} \right)^2} - \left( {x - 3} \right)\left( {x + 3} \right) = 6\) \({x^2} - 4x + 4 - \left( {{x^2} - 9} \right) = 6\) \({x^2} - 4x + 4 - {x^2} + 9 = 6\) \(\left( {{x^2} - {x^2}} \right) - 4x = 6 - 4 - 9\) \( - 4x = - 7\) \(x = \frac{7}{4}\) Vậy \(x = \frac{7}{4}.\) |
b) \(2x\left( {x - 3} \right) - 5\left( {3 - x} \right) = 0\) \(2x\left( {x - 3} \right) + 5\left( {x - 3} \right) = 0\) \(\left( {x - 3} \right)\left( {2x + 5} \right) = 0\) Suy ra \(x - 3 = 0\) hoặc \(2x + 5 = 0\) \(x = 3\) hoặc \(2x = - 5\) \(x = 3\) hoặc \(x = - \frac{5}{2}.\) Vậy \(x \in \left\{ {3; - \frac{5}{2}} \right\}.\) |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
D. Nhiệt độ trung bình (°C) của các ngày trong năm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.