PHẦN II. TỰ LUẬN (8,0 điểm)

(2,0 điểm) Thực hiện phép tính (tính hợp lí nếu có thể):

a) \(\frac{2}{9} - \frac{5}{7}\,\,.\,\,\frac{{14}}{3}\);                                                             

b) \[\frac{3}{2}\,\,.\,\,\frac{1}{5} + \frac{3}{2}\,\,.\,\,\frac{4}{5} - \frac{7}{4}\];

c) \[{\left( {\frac{{ - 4}}{7}} \right)^2}:{\left( {\frac{{ - 2}}{7}} \right)^2} + 6\,\,.\,\,\left( {\frac{{ - 1}}{6}} \right) - \sqrt {\frac{4}{{25}}} \];                              

d) \(\sqrt {\frac{1}{{25}}} \,\,.\,\,{( - 2)^2} - \sqrt {\frac{1}{{81}}} :{\left( {\frac{{ - 2}}{3}} \right)^3}\).

Gọi số tiền ban đầu là \({T_0}\).

Lãi suất theo kì hạn là \(r\).

Số tiền rút ra sau \(n\) kì hạn là: \({T_n} = {T_0}{(1 + r)^n}\).

Do kì hạn 3 tháng nên 2 năm tương ứng với số kì hạn là:

\(n = 2\,\,.\,\,12:3 = 8\) (kì hạn).

Với \({T_0} = 50{\rm{ }}000{\rm{ }}000\) đồng, \(r = 1,5\% \), \(n = 8\), ta được số tiền cô Liên rút được sau 2 năm là:

\(50{\rm{ }}000{\rm{ }}000\,.\,\,{(1 + 1,5)^8} \approx 76\,\,294\,\,000\) (đồng).

Vậy số tiền cô Liên rút được sau 2 năm khoảng 76 294 000 đồng.

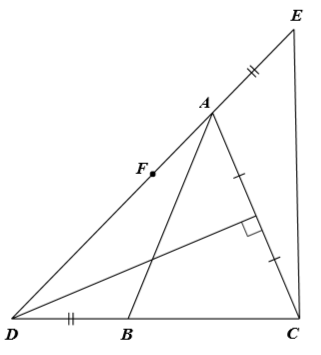
a) Theo đề bài, đường trung trực của cạnh \(AC\) cắt tia \(CB\) tại điểm \(D\).

Suy ra \(D\) thuộc đường trung trực của \(AC\) nên \(DA = DC\).

Do đó tam giác \(ADC\) có \(DA = DC\) nên tam giác \(ADC\) cân tại \(D\).

b) Vì tam giác \(ADC\) cân nên \(\widehat {DAC} = \widehat {DCA}\) (1)

Vì \(AB = AC\) nên \(\widehat {ABC} = \widehat {DCA}\) (2)

Từ (1) và (2) suy ra \(\widehat {DAC} = \widehat {ABC}\).

Ta có \(\widehat {EAC} + \widehat {DAC} = 180^\circ \); \(\widehat {DBA} + \widehat {ABC} = 180^\circ \) (hai góc kề bù)

Mà \(\widehat {DAC} = \widehat {DCA}\) nên \(\widehat {EAC} = \widehat {ABD}\) (đpcm).

c) Xét \(\Delta ABD\) và \(\Delta CAE\) có:

\(AE = BD\) (giả thiết);

\(\widehat {EAC} = \widehat {ABD}\) (chứng minh trên);

\(AB = AC\) (vì tam giác \(ABC\) cân tại \(A\)).

Do đó \(\Delta ABD = \Delta CAE\) (c.g.c).

Suy ra \(AD = CE\) (hai cạnh tương ứng).

Mà \(DA = DC\) (chứng minh trên) nên \(CE = CD\).

Mà \(FD = FE\) (\(F\) là trung điểm \(DE\))

Do đó \(CF\) là đường trung trực của \(DE\).