(2,0 điểm) Cho tam giác \(ABC\) cân tại \(A\) \(\left( {\widehat A < 90^\circ } \right)\). Đường trung trực của cạnh \(AC\) cắt tia \(CB\) tại điểm \(D\). Trên tia đối của tia \(AD\) lấy điểm E sao cho \(AE = BD\).
a) Chứng minh tam giác \(ADC\) cân;
b) Chứng minh \(\widehat {EAC} = \widehat {ABD}\);
c) Lấy \(F\) là trung điểm của \(DE\). Chứng minh \(CF\) là đường trung trực của \(DE\).
(2,0 điểm) Cho tam giác \(ABC\) cân tại \(A\) \(\left( {\widehat A < 90^\circ } \right)\). Đường trung trực của cạnh \(AC\) cắt tia \(CB\) tại điểm \(D\). Trên tia đối của tia \(AD\) lấy điểm E sao cho \(AE = BD\).
a) Chứng minh tam giác \(ADC\) cân;
b) Chứng minh \(\widehat {EAC} = \widehat {ABD}\);
c) Lấy \(F\) là trung điểm của \(DE\). Chứng minh \(CF\) là đường trung trực của \(DE\).
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
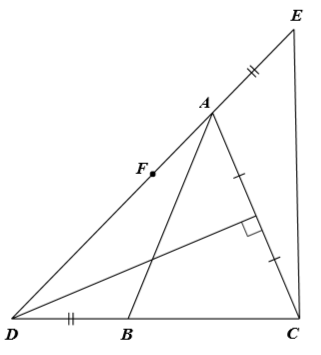
a) Theo đề bài, đường trung trực của cạnh \(AC\) cắt tia \(CB\) tại điểm \(D\).
Suy ra \(D\) thuộc đường trung trực của \(AC\) nên \(DA = DC\).
Do đó tam giác \(ADC\) có \(DA = DC\) nên tam giác \(ADC\) cân tại \(D\).
b) Vì tam giác \(ADC\) cân nên \(\widehat {DAC} = \widehat {DCA}\) (1)
Vì \(AB = AC\) nên \(\widehat {ABC} = \widehat {DCA}\) (2)
Từ (1) và (2) suy ra \(\widehat {DAC} = \widehat {ABC}\).
Ta có \(\widehat {EAC} + \widehat {DAC} = 180^\circ \); \(\widehat {DBA} + \widehat {ABC} = 180^\circ \) (hai góc kề bù)
Mà \(\widehat {DAC} = \widehat {DCA}\) nên \(\widehat {EAC} = \widehat {ABD}\) (đpcm).
c) Xét \(\Delta ABD\) và \(\Delta CAE\) có:
\(AE = BD\) (giả thiết);
\(\widehat {EAC} = \widehat {ABD}\) (chứng minh trên);
\(AB = AC\) (vì tam giác \(ABC\) cân tại \(A\)).
Do đó \(\Delta ABD = \Delta CAE\) (c.g.c).
Suy ra \(AD = CE\) (hai cạnh tương ứng).
Mà \(DA = DC\) (chứng minh trên) nên \(CE = CD\).
Mà \(FD = FE\) (\(F\) là trung điểm \(DE\))
Do đó \(CF\) là đường trung trực của \(DE\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số tiền ban đầu là \({T_0}\).
Lãi suất theo kì hạn là \(r\).
Số tiền rút ra sau \(n\) kì hạn là: \({T_n} = {T_0}{(1 + r)^n}\).
Do kì hạn 3 tháng nên 2 năm tương ứng với số kì hạn là:
\(n = 2\,\,.\,\,12:3 = 8\) (kì hạn).
Với \({T_0} = 50{\rm{ }}000{\rm{ }}000\) đồng, \(r = 1,5\% \), \(n = 8\), ta được số tiền cô Liên rút được sau 2 năm là:
\(50{\rm{ }}000{\rm{ }}000\,.\,\,{(1 + 1,5)^8} \approx 76\,\,294\,\,000\) (đồng).
Vậy số tiền cô Liên rút được sau 2 năm khoảng 76 294 000 đồng.
Lời giải
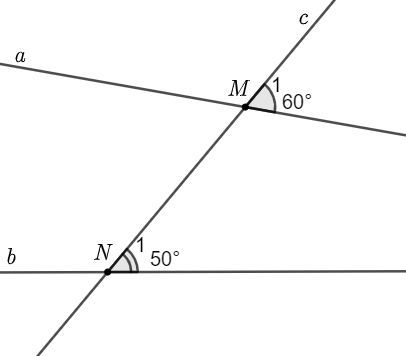
Trong hình vẽ trên, \({\widehat M_1}\) hay \({\widehat N_1}\) là hai góc đồng vị.
Mà \({\widehat M_1} \ne {\widehat N_1}\) nên hai đường thẳng \(a\) và \(b\) không song song với nhau.
Để \[a\parallel b\] thì \({\widehat M_1} = {\widehat N_1}\), tức là \({\widehat M_1} = 50^\circ \) hoặc \[{\widehat N_1} = 60^\circ \].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.