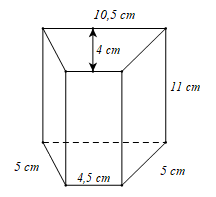
(1,0 điểm) Cho hình lăng trụ đứng có đáy là hình thang cân với các kích thước như hình vẽ. Tính diện tích xung quanh và thể tích của hình lăng trụ đó.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Chu vi đáy của hình lăng trụ đứng là:
Diện tích xung quanh của hình lăng trụ đó là: .
Diện tích đáy của hình lăng trụ đứng là:
Thể tích của hình lăng trụ đó là: .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
(2,0 điểm) Cho hình vẽ. Biết \(Ax\,{\rm{//}}\,a\).
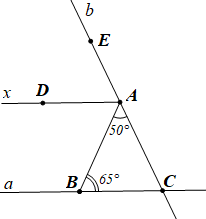
a) Vẽ lại hình (đúng số đo các góc) và viết giả thiết, kết luận của bài toán.
b) Tính số đo của \(\widehat {BAD}\) và \(\widehat {DAE}\).
c) Chứng minh \(AD\) là tia phân giác của góc \(BAE\).
d) Lấy điểm \(F\) nằm khác phía đối với điểm \(D\) so với đường thẳng \(EC\) sao cho \(\widehat {CAF} = 65^\circ \). Chứng minh ba điểm \(A,\,D,\,F\) thẳng hàng.
(2,0 điểm) Cho hình vẽ. Biết \(Ax\,{\rm{//}}\,a\).

a) Vẽ lại hình (đúng số đo các góc) và viết giả thiết, kết luận của bài toán.
b) Tính số đo của \(\widehat {BAD}\) và \(\widehat {DAE}\).
c) Chứng minh \(AD\) là tia phân giác của góc \(BAE\).
d) Lấy điểm \(F\) nằm khác phía đối với điểm \(D\) so với đường thẳng \(EC\) sao cho \(\widehat {CAF} = 65^\circ \). Chứng minh ba điểm \(A,\,D,\,F\) thẳng hàng.
Lời giải
a) Học sinh vẽ lại hình theo đúng số đo các góc.
|
GT |
\(a,\,\,b\) là các đường thẳng; Tia \(Ax\,{\rm{//}}\,a\), \(\widehat {ABC} = 65^\circ \), \(\widehat {BAC} = 50^\circ \). d) \(F\) khác phía đối với điểm \(D\) so với đường thẳng \(EC\), \(\widehat {CAF} = 65^\circ \) |
|
KL |
b) Tính \(\widehat {BAD}\) và \(\widehat {DAE}\). c) \(AD\) là tia phân giác của góc \(BAE\). d) Ba điểm \(A,\,D,\,F\) thẳng hàng. |
b) Do \[Ax\,{\rm{//}}\,a\] nên \(\widehat {BAD} = \widehat {ABC} = 65^\circ \) (hai góc so le trong).
Ta có \(\widehat {BAC} + \widehat {BAD} + \widehat {DAE} = 180^\circ \)
Suy ra \(\widehat {DAE} = 180^\circ - \widehat {BAC} - \widehat {BAD} = 180^\circ - 50^\circ - 65^\circ = 65^\circ \).
c) Do \(\widehat {BAD} = \widehat {DAE}\) (cùng bằng \(65^\circ \)) mà tia \(AD\) nằm giữa hai tia \(AB\) và \(AE\)
Suy ra tia \(AD\) là tia phân giác của góc \(BAE\).
d) Cách 1:
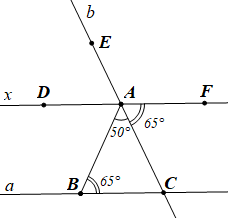
Ta có \[\widehat {DAF} = \widehat {DAB} + \widehat {BAC} + \widehat {CAF} = 65^\circ + 50^\circ + 65^\circ = 180^\circ \].
Do đó \(\widehat {DAF} = 180^\circ \) là góc bẹt, hay tia \(AD\) và tia \(AF\) là hai tia đối nhau.
Suy ra ba điểm \(A,\,D,\,F\) thẳng hàng.
Cách 2:
Do \[Ax\,{\rm{//}}\,a\] nên \(\widehat {BCA} = \widehat {DAE} = 65^\circ \) (hai góc đồng vị)
Do đó \[\widehat {CAF} = \widehat {BCA}\] (cùng bằng \(65^\circ \))
Mà hai góc này ở vị trí so le trong nên \(AF\,{\rm{//}}\,a\)
Ta có: qua điểm \(A\) có hai đường thẳng \[AD\] và \(AF\) cùng song song với \(a\) nên theo Tiên đề Euclid ta có hai đường thẳng \[AD\] và \(AF\) trùng nhau.
Vậy ba điểm \(A,\,D,\,F\) thẳng hàng.
Lời giải
Ta có: \(3{\left( {x - 2023} \right)^2} + {y^2} = 16\)
Suy ra \(3{\left( {x - 2023} \right)^2} = 16 - {y^2}\)
• Với mọi \(x \in \mathbb{Z}\) ta có \(3{\left( {x - 2023} \right)^2} \ge 0\)
\( \Rightarrow 16 - {y^2} \ge 0\) với mọi \(y \in \mathbb{Z}\)
\( \Rightarrow {y^2} \le 16\) với mọi \(y \in \mathbb{Z}\)
• Do \(x \in \mathbb{Z}\) nên \(3{\left( {x - 2023} \right)^2} \vdots 3\)
\( \Rightarrow \left( {16 - {y^2}} \right) \vdots 3\) hay \(\left( {{y^2} - 16} \right) \vdots 3\)
Do đó \({y^2}\) chia \(3\) dư \(1\)
Từ đó ta có \({y^2}\) là số chính phương thỏa mãn \({y^2} \le 16,{y^2}\) chia \(3\) dư \(1\)
Suy ra \({y^2} \in \left\{ {1;4;16} \right\}\)
• Với \({y^2} = 1\) ta có \(3{\left( {x - 2023} \right)^2} = 16 - 1 = 15\)
\({\left( {x - 2023} \right)^2} = 5\) (loại vì \(x \in \mathbb{Z}\))
• Với \({y^2} = 4\) ta có \(3{\left( {x - 2023} \right)^2} = 16 - 4 = 12\)
\({\left( {x - 2023} \right)^2} = 4\)
Suy ra \(x - 2023 = 2\) hoặc \(x - 2023 = - 2\)
Do đó \(x = 2025\) hoặc \(x = 2021\).
Từ \({y^2} = 4\) suy ra \(y = 2\) hoặc \(y = - 2\).
• Với \({y^2} = 16\) ta có \(3{\left( {x - 2023} \right)^2} = 16 - 16 = 0\)
\({\left( {x - 2023} \right)^2} = 0\)
\(x - 2023 = 0\)
\(x = 2023\).
Từ \({y^2} = 16\)suy ra \(y = 4\) hoặc \(y = - 4\).
Vậy các cặp số \(\left( {x;y} \right)\) thỏa mãn là \[\left( {2025;2} \right);\left( {2025; - 2} \right);\left( {2021;2} \right);\left( {2021; - 2} \right);\]\(\left( {2023;4} \right);\)\(\left( {2023; - 4} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.