(2,0 điểm) Cho hình vẽ. Biết \(Ax\,{\rm{//}}\,a\).
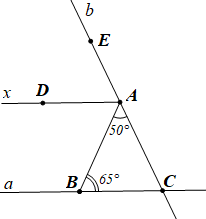
a) Vẽ lại hình (đúng số đo các góc) và viết giả thiết, kết luận của bài toán.
b) Tính số đo của \(\widehat {BAD}\) và \(\widehat {DAE}\).
c) Chứng minh \(AD\) là tia phân giác của góc \(BAE\).
d) Lấy điểm \(F\) nằm khác phía đối với điểm \(D\) so với đường thẳng \(EC\) sao cho \(\widehat {CAF} = 65^\circ \). Chứng minh ba điểm \(A,\,D,\,F\) thẳng hàng.
(2,0 điểm) Cho hình vẽ. Biết \(Ax\,{\rm{//}}\,a\).

a) Vẽ lại hình (đúng số đo các góc) và viết giả thiết, kết luận của bài toán.
b) Tính số đo của \(\widehat {BAD}\) và \(\widehat {DAE}\).
c) Chứng minh \(AD\) là tia phân giác của góc \(BAE\).
d) Lấy điểm \(F\) nằm khác phía đối với điểm \(D\) so với đường thẳng \(EC\) sao cho \(\widehat {CAF} = 65^\circ \). Chứng minh ba điểm \(A,\,D,\,F\) thẳng hàng.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
a) Học sinh vẽ lại hình theo đúng số đo các góc.
|
GT |
\(a,\,\,b\) là các đường thẳng; Tia \(Ax\,{\rm{//}}\,a\), \(\widehat {ABC} = 65^\circ \), \(\widehat {BAC} = 50^\circ \). d) \(F\) khác phía đối với điểm \(D\) so với đường thẳng \(EC\), \(\widehat {CAF} = 65^\circ \) |
|
KL |
b) Tính \(\widehat {BAD}\) và \(\widehat {DAE}\). c) \(AD\) là tia phân giác của góc \(BAE\). d) Ba điểm \(A,\,D,\,F\) thẳng hàng. |
b) Do \[Ax\,{\rm{//}}\,a\] nên \(\widehat {BAD} = \widehat {ABC} = 65^\circ \) (hai góc so le trong).
Ta có \(\widehat {BAC} + \widehat {BAD} + \widehat {DAE} = 180^\circ \)
Suy ra \(\widehat {DAE} = 180^\circ - \widehat {BAC} - \widehat {BAD} = 180^\circ - 50^\circ - 65^\circ = 65^\circ \).
c) Do \(\widehat {BAD} = \widehat {DAE}\) (cùng bằng \(65^\circ \)) mà tia \(AD\) nằm giữa hai tia \(AB\) và \(AE\)
Suy ra tia \(AD\) là tia phân giác của góc \(BAE\).
d) Cách 1:
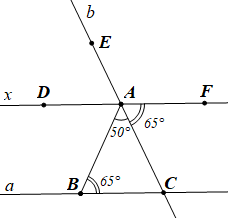
Ta có \[\widehat {DAF} = \widehat {DAB} + \widehat {BAC} + \widehat {CAF} = 65^\circ + 50^\circ + 65^\circ = 180^\circ \].
Do đó \(\widehat {DAF} = 180^\circ \) là góc bẹt, hay tia \(AD\) và tia \(AF\) là hai tia đối nhau.
Suy ra ba điểm \(A,\,D,\,F\) thẳng hàng.
Cách 2:
Do \[Ax\,{\rm{//}}\,a\] nên \(\widehat {BCA} = \widehat {DAE} = 65^\circ \) (hai góc đồng vị)
Do đó \[\widehat {CAF} = \widehat {BCA}\] (cùng bằng \(65^\circ \))
Mà hai góc này ở vị trí so le trong nên \(AF\,{\rm{//}}\,a\)
Ta có: qua điểm \(A\) có hai đường thẳng \[AD\] và \(AF\) cùng song song với \(a\) nên theo Tiên đề Euclid ta có hai đường thẳng \[AD\] và \(AF\) trùng nhau.
Vậy ba điểm \(A,\,D,\,F\) thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
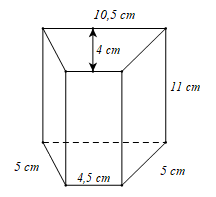
Chu vi đáy của hình lăng trụ đứng là:
Diện tích xung quanh của hình lăng trụ đó là: .
Diện tích đáy của hình lăng trụ đứng là:
Thể tích của hình lăng trụ đó là: .
Lời giải
Ta có: \(3{\left( {x - 2023} \right)^2} + {y^2} = 16\)
Suy ra \(3{\left( {x - 2023} \right)^2} = 16 - {y^2}\)
• Với mọi \(x \in \mathbb{Z}\) ta có \(3{\left( {x - 2023} \right)^2} \ge 0\)
\( \Rightarrow 16 - {y^2} \ge 0\) với mọi \(y \in \mathbb{Z}\)
\( \Rightarrow {y^2} \le 16\) với mọi \(y \in \mathbb{Z}\)
• Do \(x \in \mathbb{Z}\) nên \(3{\left( {x - 2023} \right)^2} \vdots 3\)
\( \Rightarrow \left( {16 - {y^2}} \right) \vdots 3\) hay \(\left( {{y^2} - 16} \right) \vdots 3\)
Do đó \({y^2}\) chia \(3\) dư \(1\)
Từ đó ta có \({y^2}\) là số chính phương thỏa mãn \({y^2} \le 16,{y^2}\) chia \(3\) dư \(1\)
Suy ra \({y^2} \in \left\{ {1;4;16} \right\}\)
• Với \({y^2} = 1\) ta có \(3{\left( {x - 2023} \right)^2} = 16 - 1 = 15\)
\({\left( {x - 2023} \right)^2} = 5\) (loại vì \(x \in \mathbb{Z}\))
• Với \({y^2} = 4\) ta có \(3{\left( {x - 2023} \right)^2} = 16 - 4 = 12\)
\({\left( {x - 2023} \right)^2} = 4\)
Suy ra \(x - 2023 = 2\) hoặc \(x - 2023 = - 2\)
Do đó \(x = 2025\) hoặc \(x = 2021\).
Từ \({y^2} = 4\) suy ra \(y = 2\) hoặc \(y = - 2\).
• Với \({y^2} = 16\) ta có \(3{\left( {x - 2023} \right)^2} = 16 - 16 = 0\)
\({\left( {x - 2023} \right)^2} = 0\)
\(x - 2023 = 0\)
\(x = 2023\).
Từ \({y^2} = 16\)suy ra \(y = 4\) hoặc \(y = - 4\).
Vậy các cặp số \(\left( {x;y} \right)\) thỏa mãn là \[\left( {2025;2} \right);\left( {2025; - 2} \right);\left( {2021;2} \right);\left( {2021; - 2} \right);\]\(\left( {2023;4} \right);\)\(\left( {2023; - 4} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.