Thống kê phương tiện đi đến trường của 30 học sinh lớp 7B ta thu được bảng sau:

Phương tiện đi lại	Số học sinh
Đi bộ	5
Đi xe đạp	10
Đi xe máy	15
Đi xe buýt	5
Tổng cộng	35

Giá trị chưa hợp lí là:

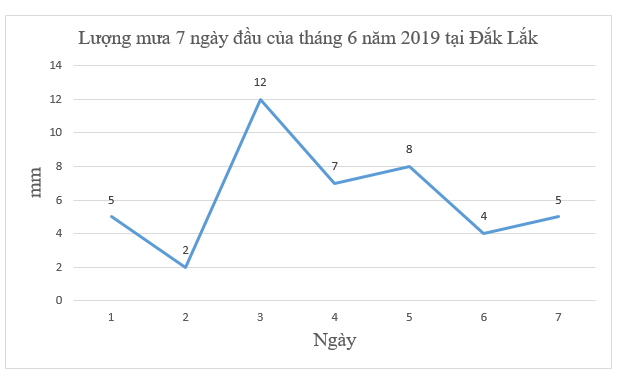
a) Biểu đồ trên thể hiện thông tin là: Lượng mưa 7 ngày đầu của tháng 6 năm 2019 tại Đắk Lắk.

b) Ta thấy: Ngày thứ nhất lượng mưa là 5 mm.

Ngày thứ hai lượng mưa là 2 mm.

Ngày thứ ba lượng mưa là 12 mm.

Ngày thứ tư lượng mưa là 7 mm.

Ngày thứ năm lượng mưa là 8 mm.

Ngày thứ sáu lượng mưa là 4 mm.

Ngày thứ bảy lượng mưa là 5 mm.

Những ngày có lượng mưa lớn hơn 6 mm là: Ngày thứ ba (12 mm); ngày thứ tư (7 mm); ngày thứ năm (8 mm).

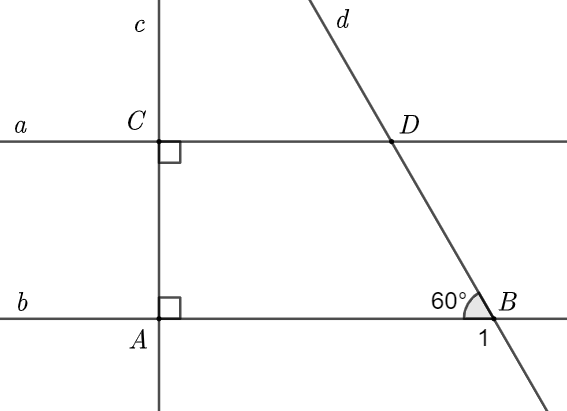
a) Quan sát hình vẽ ta thấy: \(a \bot c;\,\,b \bot c\).

Do đó \[a\parallel b\].

b) Vì \(\widehat {DBA}\) và \(\widehat {{B_1}}\) là hai góc kề bù nên \(\widehat {DBA} + \widehat {{B_1}} = 180^\circ \)

Hay \(60^\circ + \widehat {{B_1}} = 180^\circ \)

Do đó \(\widehat {{B_1}} = 180^\circ - 60^\circ = 120^\circ \)

Mặt khác, \[a\parallel b\] nên \(\widehat {{B_1}} = \widehat {CDB} = 120^\circ \) (hai góc đồng vị).

Vậy \(\widehat {CDB} = 120^\circ \).