(1,0 điểm) Trong ngày hội việc làm ở thành phố Hà Nội, người ta thống kê có 10 350 lượt người tham gia. Hãy làm tròn số này với độ chính xác \(d = 50\).
(1,0 điểm) Trong ngày hội việc làm ở thành phố Hà Nội, người ta thống kê có 10 350 lượt người tham gia. Hãy làm tròn số này với độ chính xác \(d = 50\).
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Làm tròn 10 350 với độ chính xác \(d = 50\), tức là làm tròn số này đến hàng trăm.
Áp dụng quy tắc làm tròn ta được \[10\,\,350 \approx 10\,\,400\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
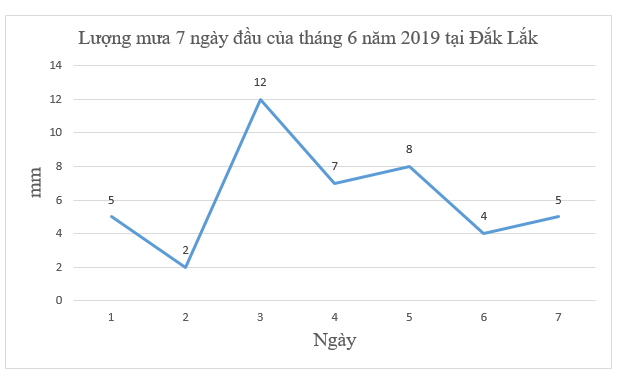
a) Biểu đồ trên thể hiện thông tin là: Lượng mưa 7 ngày đầu của tháng 6 năm 2019 tại Đắk Lắk.
b) Ta thấy: Ngày thứ nhất lượng mưa là 5 mm.
Ngày thứ hai lượng mưa là 2 mm.
Ngày thứ ba lượng mưa là 12 mm.
Ngày thứ tư lượng mưa là 7 mm.
Ngày thứ năm lượng mưa là 8 mm.
Ngày thứ sáu lượng mưa là 4 mm.
Ngày thứ bảy lượng mưa là 5 mm.
Những ngày có lượng mưa lớn hơn 6 mm là: Ngày thứ ba (12 mm); ngày thứ tư (7 mm); ngày thứ năm (8 mm).
Lời giải
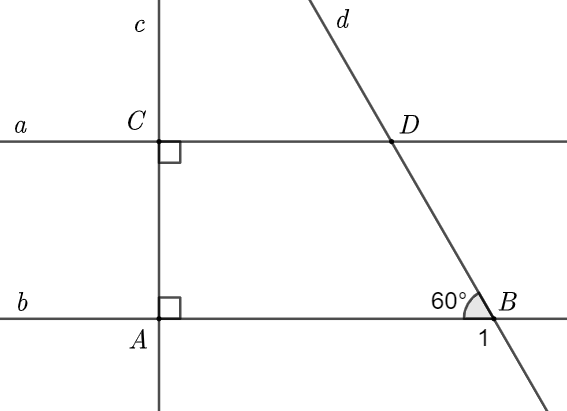
a) Quan sát hình vẽ ta thấy: \(a \bot c;\,\,b \bot c\).
Do đó \[a\parallel b\].
b) Vì \(\widehat {DBA}\) và \(\widehat {{B_1}}\) là hai góc kề bù nên \(\widehat {DBA} + \widehat {{B_1}} = 180^\circ \)
Hay \(60^\circ + \widehat {{B_1}} = 180^\circ \)
Do đó \(\widehat {{B_1}} = 180^\circ - 60^\circ = 120^\circ \)
Mặt khác, \[a\parallel b\] nên \(\widehat {{B_1}} = \widehat {CDB} = 120^\circ \) (hai góc đồng vị).
Vậy \(\widehat {CDB} = 120^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.