khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Vào học
Đăng nhập
Tạo VIP
Xin chào! Vào học
  2. Lớp 7
  3. Toán

Câu hỏi:

23/11/2025 397 Lưu

(1,75 điểm) Một xe container có thùng xe dạng hình hộp chữ nhật có chiều dài \[2,8\,\,{\rm{m}}\]; chiều rộng \[2,3\,\,{\rm{m}}\] và diện tích xung quanh là \[24,48{\rm{ }}\,\,{{\rm{m}}^2}\].

a) Tính thể tích của thùng xe container đó.

b) Xe container cần chở các thùng hàng dạng hình lăng trụ đứng tam giác có các kích thước như hình vẽ. Nếu người khuân vác biết cách sắp xếp hợp lí thì xe container có thể chở tối đa bao nhiêu thùng hàng?

Xem lời giải

Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Chân trời sáng tạo có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

a) Chu vi đáy của thùng xe container đó là: Cđáy=2.2,8+2,3=10,2  m .

Chiều cao của thùng xe container đó là: h=SxqCđáy=24,4810,2=2,4   m .

Diện tích đáy của thùng xe container đó là: Sđáy=2,8.2,3=6,44  m2.

Thể tích của thùng xe container đó là: V=Sđáy.h=6,44.2,4=15,456  m3.

b) Đổi: \(80\,\,cm = 0,8\,\,m\); \(60\,\,cm = 0,6\,\,m\); \(50\,\,cm = 0,5\,\,m\).

Thể tích mỗi thùng hàng là: \(\left( {\frac{1}{2}.0,6.0,5} \right).0,8 = 0,12\,\left( {{m^3}} \right)\).

Nếu người khuân vác biết cách sắp xếp hợp lí thì xe container có thể chở tối đa số thùng hàng là: \(15,456:0,12 = 128,8\) (thùng hàng).

Vậy nếu người khuân vác biết cách sắp xếp hợp lí thì xe container có thể chở tối đa 128 thùng hàng.

Đang tải chế độ Học...

Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

(0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức \(A = {\left( {\left| {x - 5} \right| + 3} \right)^2} + \left| {y + 4} \right| + 2022\).

Lời giải

Ta có \(\left| {x - 5} \right| \ge 0\), với mọi \(x\)

\( \Rightarrow \left| {x - 5} \right| + 3 \ge 3\), với mọi \(x\)

\( \Rightarrow {\left( {\left| {x - 5} \right| + 3} \right)^2} \ge {3^2} = 9\), với mọi \(x\)

Lại có \(\left| {y + 4} \right| \ge 0\), với mọi \(y\)

\[ \Rightarrow {\left( {\left| {x - 5} \right| + 3} \right)^2} + \left| {y + 4} \right| \ge 9\].

\( \Rightarrow {\left( {\left| {x - 5} \right| + 3} \right)^2} + \left| {y + 4} \right| + 2022 \ge 9 + 2022 = 2031\).

Vì vậy \(A \ge 2031\).

Dấu “=” xảy ra khi \(x = 5\) và \(y = - 4\).

Vậy giá trị nhỏ nhất của \(A\) là 2031 khi \(x = 5\) và \(y = - 4\).

Câu 2

Trong các phân số sau, phân số nào không viết được dưới dạng số thập phân hữu hạn?

A. \(\frac{5}{{72}}\);      

B. \(\frac{{10}}{{64}}\);      
C. \(\frac{{81}}{6}\);           
D. \(\frac{9}{4}\).

Lời giải

Đáp án đúng là: A

Ta có:

⦁ \[\frac{5}{{72}} = \frac{5}{{{2^3}{{.3}^2}}}\] là phân số tối giản với mẫu dương có ước nguyên tố khác 2 và 5 nên là số thập phân vô hạn tuần hoàn;

⦁ Các số\(\frac{{10}}{{64}} = \frac{5}{{32}}\); \(\frac{{81}}{6} = \frac{{27}}{2}\) và \(\frac{9}{4}\) là các phân số tối giản với mẫu dương có ước nguyên tố là 2 và 5, nên là số thập phân hữu hạn.

Vậy ta chọn phương án A.

Câu 3

(1,25 điểm) Tìm \(x\), biết:

a) \(\frac{2}{9} + \frac{4}{5}x = \frac{9}{5}\);      

b) \(\frac{5}{{11}} + \frac{2}{{11}}:\left| {\frac{3}{7} - x} \right| = \frac{4}{5}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

(1,5 điểm) Cho hình vẽ sau, biết \(\widehat {ABC} = 80^\circ \) và \(Am\,{\rm{//}}\,Cp\).

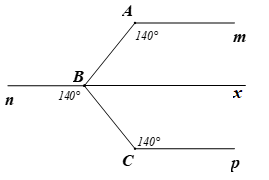
Cho hình vẽ sau, biết \(\widehat { (ảnh 1)

a) Vẽ lại hình (đúng số đo các góc) và viết giả thiết, kết luận của bài toán.

b) Giải thích tại sao hai đường thẳng \(Bn\) và \(Cp\) song song với nhau. Từ đó suy ra hai đường thẳng \(Am\) và \(Bn\) song song với nhau.

c) Kẻ \(Bx\) là tia đối của tia \(Bn\). Chứng minh \(Bx\) là tia phân giác của \(\widehat {ABC}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

PHẦN II. TỰ LUẬN (8,0 điểm)

 (1,5 điểm) Thực hiện phép tính (tính hợp lí nếu có thể):

a) \[\frac{{{{\left( {{2^4}} \right)}^3}{{.5}^9}}}{{{{25}^4}{{.2}^{11}}}}\];      

b) \(\sqrt {29 + 7} .\frac{4}{3} + \left| { - \frac{8}{3}} \right|\);     

c) \(\left( {\frac{1}{6} - \frac{5}{8}} \right).2\frac{1}{3} + \left( {\frac{5}{6} + \frac{{21}}{8}} \right):\frac{3}{7}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Dãy dữ liệu nào sau đây không là dãy dữ liệu định tính?
A. Thủ đô của một số quốc gia tại châu Á: Bắc Kinh, Phnom Pênh, Hà Nội, Seoul, Jakarta, Viêng Chăn,…;  
B. Một số thiết bị điện tử được bán trong một cửa hàng là: điện thoại, laptop, máy tính bảng, ti vi, tủ lạnh, điều hòa,…;
C. Một số địa điểm du lịch tại Việt Nam: Phú Quốc, Nha Trang, Hội An, Đà Nẵng,…;
D. Số kg giấy vụn các lớp \[7A\], \[7B\], \[7C\], \[7D\] đóng góp lần lượt là: \[25;50;65;48\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập