Giải bài toán sau bằng cách lập hệ phương trình:
Đại hội Thể thao Đông Nam Á – SEA Games (South East Asian Games) là sự kiện thể thao được tổ chức 2 năm 1 lần với sự tham gia của các vận động viên trong khu vực Đông Nam Á. Việt Nam là đội chủ nhà của SEA Games 31 diễn ra từ ngày 12/5/2022 đến ngày 23/5/2022. Ở môn bóng đá nam, một bảng đấu có 5 đội A, B, C, D, E thi đấu theo thể thức vòng tròn một lượt (mỗi đội thi đấu đúng một trận với các đội còn lại).

Trong mỗi trận đấu, đội thắng được 3 điểm, đội hòa được 1 điểm và đội thua được 0 điểm. Khi kết thúc bảng đấu, các đội A, B, C, D, E lần lượt có điểm số là \(10\,;\,\,9\,;\,\,6\,;\,\,4\,;\,\,0.\) Hỏi có bao nhiêu trận hòa và cho biết đó là trận hòa giữa các đội nào (nếu có)?

Trong mỗi trận đấu, đội thắng được 3 điểm, đội hòa được 1 điểm và đội thua được 0 điểm. Khi kết thúc bảng đấu, các đội A, B, C, D, E lần lượt có điểm số là \(10\,;\,\,9\,;\,\,6\,;\,\,4\,;\,\,0.\) Hỏi có bao nhiêu trận hòa và cho biết đó là trận hòa giữa các đội nào (nếu có)?
Quảng cáo
Trả lời:
Gọi \(x\) là số trận thắng – thua và \(y\) là số trận hòa \[\left( {x,{\rm{ }}y \in \mathbb{N}*} \right)\].
Nếu có 5 đội tham gia thi đấu, mỗi đội phải đấu với 4 đội còn lại nên với 5 đội tham gia thì có \(5 \cdot 4 = 20\) (trận đấu). Nhưng mỗi trận đấy có 2 đội tham gia nên tổng số trận đấu khi có 5 đội tham gia là \(\frac{{5 \cdot 4}}{2} = 10\) (trận đấu).
Vì có 10 trận đấu nên \(x + y = 10 & \left( 1 \right)\)
Mặt khác, tổng số điểm các đội là \(10 + 9 + 6 + 4 + 0 = 29\) (điểm).
Mỗi trận thắng – thua có tổng số điểm là 3 và mỗi trận hòa có tổng số có tổng số điểm là 2 nên ta có phương trình \(3x + 2y = 29 & \left( 2 \right)\)
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 10\\3x + 2y = 29\end{array} \right.\).
Từ phương trình thứ hai ta có \(x + y = 10\) suy ra \(x = 10 - y\). Thế vào phương trình thứ nhất, ta được:
\(3\left( {10 - y} \right) + 2y = 29\), suy ra \(30 - 3y + 2y = 29\) hay \(y = 1\) (thỏa mãn).
Từ đó \(x = 10 - y = 10 - 1 = 9\) (thỏa mãn).
Mỗi đội có 4 trận đấu với các đội còn lại mà đội A có 10 điểm tức đội A thắng 3 trận hòa 1 trận.
Đội B có 9 điểm tức thắng 3 trận thua 1 trận.
Đội C có 6 điểm tức thắng 2 trận thua 2 trận.
Đội D có 4 điểm thắng 1 trận hòa 1 trận.
Đội E không có điểm tức là thua hết 4 trận.
Vậy trận hòa là của đội A và đội D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đến ngày 31/12/2024, gia đình cô Thúy đã tiết kiệm được số tiền là 250 triệu đồng. Sau thời điểm đó, mỗi tháng gia đình cô Thúy đều tiết kiệm được 10 triệu đồng. Gia đình cô Thúy dự định mua một chiếc ô tô tải nhỏ để vận chuyển hàng hóa với giá để vận chuyển hàng hoá với giá tối thiểu là 370 triệu đồng.
a) Gọi \(x\) (tháng) là thời gian gia đình cô Thúy có thể mua được chiếc ô tô tải bằng tiền tiết kiệm được \(\left( {x > 0} \right)\). Viết bất phương trình phù hợp với dữ liệu đề bài.
b) Hỏi sau ít nhất bao nhiêu tháng gia đình cô Thúy có thể mua được chiếc ô tô tải đó bằng số tiền tiết kiệm được?
Đến ngày 31/12/2024, gia đình cô Thúy đã tiết kiệm được số tiền là 250 triệu đồng. Sau thời điểm đó, mỗi tháng gia đình cô Thúy đều tiết kiệm được 10 triệu đồng. Gia đình cô Thúy dự định mua một chiếc ô tô tải nhỏ để vận chuyển hàng hóa với giá để vận chuyển hàng hoá với giá tối thiểu là 370 triệu đồng.
a) Gọi \(x\) (tháng) là thời gian gia đình cô Thúy có thể mua được chiếc ô tô tải bằng tiền tiết kiệm được \(\left( {x > 0} \right)\). Viết bất phương trình phù hợp với dữ liệu đề bài.
b) Hỏi sau ít nhất bao nhiêu tháng gia đình cô Thúy có thể mua được chiếc ô tô tải đó bằng số tiền tiết kiệm được?
Lời giải
a) Gọi \(x\) (tháng) là thời gian gia đình cô Thúy có thể mua được chiếc ô tô tải bằng tiền tiết kiệm được \(\left( {x > 0} \right)\).
Sau x tháng, số tiền gia đình cô Thúy tiết kiệm được là: \[10x\] (triệu đồng).
Khi đó tổng số tiền gia đình cô Thúy tiết kiệm được là: \[250 + 10x\] (triệu đồng).
Theo bài, gia đình cô Thúy dự định mua một chiếc ô tô tải nhỏ để vận chuyển hàng hoá với giá tối thiểu là 370 triệu đồng nên ta có bất phương trình: \[250 + 10x \ge 370.\]
Vậy bất phương trình cần tìm là: \[250 + 10x \ge 370.\]
b) Giải bất phương trình:
\[250 + 10x \ge 370\]
\[10x \ge 120\]
\[x \ge 12.\]
Vậy sau ít nhất 12 tháng, gia đình cô Thúy có thể mua được chiếc ô tô tải đó bằng số tiền tiết kiệm được.
Lời giải
Quãng đường chiếc thuyền đi được giữa hai lần quan sát là \(CD.\)
Xét \(\Delta BAC\) vuông tại \(A\) có
\(AC = 75\cot \widehat {BCA} = 75\cot 45^\circ = 75\,\,\left( {\rm{m}} \right)\).
Xét \(\Delta DAB\) vuông tại \(A\) có
\(AD = 75\cot \widehat {BDA} = 75\cot 30^\circ = 75\sqrt 3 \,\,\left( {\rm{m}} \right)\).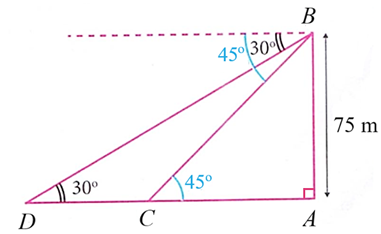
Quãng đường chiếc thuyền đi được giữa hai lần quan sát là:
\(CD = AD - AC = 75\sqrt 3 - 75 \approx 55\,\,\left( {\rm{m}} \right)\).
Vậy chiếc thuyền đi được khoảng 55 mét giữa hai lần quan sát.
Câu 3
Cho tam giác nhọn \[ABC\] có đường cao \[AK\].
a) Viết các tỉ số lượng giác của góc \(C.\)
b) Chứng minh rằng \[AK = \frac{{BC}}{{\cot B + \cot C}}\].
c) Vẽ hình chữ nhật \[CKAD\], \[BD\] cắt \[AK\] tại \[N\]. Chứng minh rằng \[\frac{1}{{A{K^2}}} = \frac{{{{\cot }^2}ACB}}{{D{N^2}}} + \frac{1}{{D{B^2}}}\].
Cho tam giác nhọn \[ABC\] có đường cao \[AK\].
a) Viết các tỉ số lượng giác của góc \(C.\)
b) Chứng minh rằng \[AK = \frac{{BC}}{{\cot B + \cot C}}\].
c) Vẽ hình chữ nhật \[CKAD\], \[BD\] cắt \[AK\] tại \[N\]. Chứng minh rằng \[\frac{1}{{A{K^2}}} = \frac{{{{\cot }^2}ACB}}{{D{N^2}}} + \frac{1}{{D{B^2}}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.