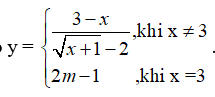Cho hình chóp \[S.ABCD\,\], đáy \[ABCD\] là hình vuông có cạnh bằng 6. Trên các cạnh \[SA,SB\] lần lượt lấy \[M,N\] sao cho \[\frac{{SM}}{{SA}} = \frac{2}{3}\], \[\frac{{SN}}{{SB}} = \frac{2}{3}.\]
a. Chứng minh rằng\[MN\,{\rm{//}}\,\left( {ABCD} \right)\].
b. Một mặt phẳng \[\left( \alpha \right)\] đi qua \[M,N\] song song với \[AB\] và \[BC\]. Tính diện tích thiết diện của \[\left( \alpha \right)\] và hình chóp.
Quảng cáo
Trả lời:
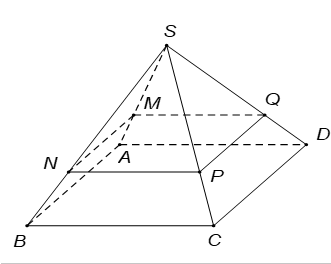
a. Ta có \[\frac{{SM}}{{SA}} = \frac{2}{3}\], \[\frac{{SN}}{{SB}} = \frac{2}{3}.\]\[ \Rightarrow \]\[MN\]//\[AB\]\[ \Rightarrow MN//\left( {ABCD} \right).\]
b. Ta có \[\left( \alpha \right)\parallel AB\] và \[BC\] suy ra \[\left( \alpha \right)\parallel \left( {ABCD} \right).\]
Giả sử \[\left( \alpha \right)\] cắt các mặt bên \[\left( {SAB} \right),\,\,\left( {SBC} \right),\,\,\left( {SCD} \right),\,\,\left( {SDA} \right)\] lần lượt tại các điểm M, \[N,\,\,P,\,\,Q\] với \[N \in SB,\,\,P \in SC,\,\,Q \in SD\,\]suy ra \[\left( \alpha \right) \equiv \left( {MNPQ} \right)\,.\]
Khi đó \[MN\]//\[AB\]\[ \Rightarrow \,\,\,\frac{{SM}}{{SA}} = \frac{{MN}}{{AB}} = \frac{2}{3}\,.\]
Tương tự, ta có được \[\frac{{NP}}{{BC}} = \frac{{PQ}}{{CD}} = \frac{{QM}}{{DA}} = \frac{2}{3}\] và \[MNPQ\] là hình vuông.
Suy ra \[{S_{MNPQ}} = {\left( {\frac{2}{3}} \right)^2}{S_{ABCD}} = \frac{4}{9}{S_{ABCD}} = \frac{4}{9}.6.6 = 16.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn A
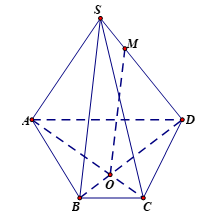
Ta có \(AD\,{\rm{//}}\,BC,AD = 2BC,AC \cap BD = O \Rightarrow \frac{{BC}}{{AD}} = \frac{{OC}}{{OA}} = \frac{{OB}}{{OD}} = \frac{1}{2}\).
Mà \(MD = 2MS \Rightarrow \frac{{MS}}{{MD}} = \frac{1}{2}\).
Suy ra \(\frac{{OB}}{{OD}} = \frac{{MS}}{{MD}} = \frac{1}{2} \Rightarrow OM\,{\rm{//}}\,SB\), mà \(SB \subset \left( {SAB} \right)\) nên \(OM\,{\rm{//}}\,\left( {SAB} \right)\).
Câu 2
Lời giải
Chọn B
Tần số lớn nhất là 120 nên nhóm chứa mốt là nhóm \(\left[ {18;20} \right)\).
Ta có \(j = 3;{a_3} = 18;{m_3} = 120;{m_2} = 78;{m_4} = 45;h = 4\).
Do đó \({M_0} = 18 + \frac{{120 - 78}}{{\left( {120 - 78} \right) + \left( {120 - 45} \right)}}.4 = \frac{{758}}{{39}}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.