Trong hộp có 1 quả bóng được đánh số 1; 2 quả bóng được đánh số 2; 3 quả bóng được đánh số 3 ; …; 30 quả bóng được đánh số 30 . Ta lấy bóng từ trong hộp ra mà không nhìn. Phải lấy ít nhất bao nhiêu quả để đảm bảo trong đó có 10 quả bóng có số giống nhau?
Quảng cáo
Trả lời:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
a) Nếu chuyển \(\frac{1}{6}\)số kẹo ở túi thứ nhất sang túi thứ hai thì số kẹo ở túi thứ nhất lúc sau
bằng \(\frac{5}{6}\)số kẹo ở túi thứ nhất lúc đầu.
Vì số kẹo ở túi thứ hai lúc sau bằng \(\frac{{11}}{{10}}\)số kẹo ở túi thứ nhất lúc sau nên tỉ lệ số kẹo ở túi thứ hai lúc sau so với túi thứ nhất lúc đầu là: \(\frac{{11}}{{10}} \times \frac{5}{6} = \frac{{11}}{{12}}\)
Do đó, số kẹo ở túi thứ hai lúc đầu bằng \(\frac{{11}}{{12}} - \frac{1}{6} = \frac{3}{4}\) số kẹo ở túi thứ nhất lúc đầu.
Vậy tỉ số số kẹo ở túi thứ nhất và túi thứ hai là \(\frac{4}{3}\)
b) Nếu chuyển \(\frac{1}{6}\)số kẹo ở túi thứ hai sang túi thứ ba thì số kẹo ở túi thứ hai lúc sau bằng \(\frac{5}{6}\)số kẹo ở túi thứ hai lúc đầu.
Vì số kẹo ở túi thứ hai lúc sau bằng số kẹo ở túi thứ ba lúc sau nên tỉ lệ số kẹo ở túi thứ
ba lúc sau bằng \(\frac{5}{6}\)số kẹo ở túi thứ hai lúc đầu.
Do đó, số kẹo ở túi thứ ba lúc đầu bằng \(\frac{5}{6} - \frac{1}{6} = \frac{2}{3}\) số kẹo ở túi thứ hai lúc đầu.
Số kẹo ở túi thứ ba lúc đầu là: \(60:\left( {2 + 3} \right) \times 2 = 24\)(cái kẹo)
Số kẹo ở túi thứ hai lúc đầu là: 24 : 2 × 3 = 36 (cái kẹo)
Số kẹo ở túi thứ nhất lúc đầu là: 36 : 3 × 4 = 48 (cái kẹo)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
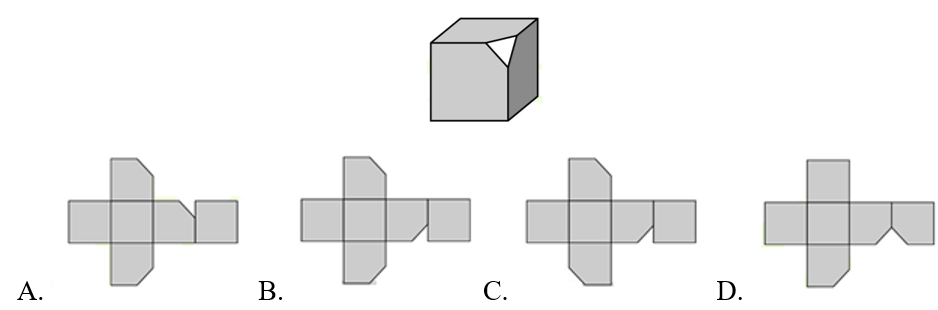
A. Hình A
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.