Một bể nước hình hộp chữ nhật có chiều dài 80 cm, chiều rộng 40 cm, chiều cao 60 cm. Hỏi bể nước chứa được bao nhiêu lít nước?
Một bể nước hình hộp chữ nhật có chiều dài 80 cm, chiều rộng 40 cm, chiều cao 60 cm. Hỏi bể nước chứa được bao nhiêu lít nước?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Bể nước chứa được số lít nước là:
80 × 40 × 60 = 192 000 (cm3)
Đổi 192 000 cm3 = 192 lít
Đáp số: 192 lít
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
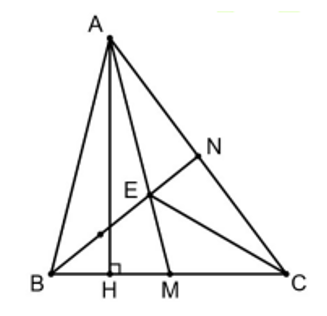
a) Vì tam giác ABE và tam giác ABN cùng chiều cao từ \(A\) và\(BE = \frac{2}{3}BN\), nên:
\({S_{ABE}} = \frac{2}{3} \times {S_{ABN}} = \frac{2}{3} \times 6 = 4\,\)(cm2)
b) Tam giác ABN và tam giác ABC có chung chiều cao hạ từ đỉnh B và AN = \(\frac{1}{2}\) AC nên: \({S_{ABN}} = \frac{1}{2}{S_{ABC}}\,\), suy ra \({S_{ABC}} = 2 \times {S_{ABN}} = 2 \times 6 = 12\)(cm2)
Ta có: \({S_{ABC}} = \frac{1}{2} \times BC \times AH\) nên \(AH = 2 \times {S_{ABC}}:BC = 2 \times 12:4 = 6\,\,({\rm{cm)}}\)
c) Ta có: \({S_{ABE}} = 2{S_{AEN}}\) (Chung chiều cao hạ từ A và BE = 2 EN)
Ta có : \({S_{AEC}} = 2{S_{AEN}}\) (Chung chiều cao hạ từ E và AC = 2 AN)
Suy ra \({S_{ABE}} = {S_{AEC}}\) , mà hai tam giác này chung đáy AE suy ra đường cao hạ từ B bằng đường cao hạ từ C xuống đáy AE, đây cũng là hai đường cao của hai tam giác ABM và ACM
Suy ra: \({S_{ABM}} = {S_{ACM}}\)(chung đáy AM, đường cao hạ từ B xuống AM bằng đường cao hạ từ C xuống AM)
Do đó, trong tam giác \(ABC\) thì: \(BM = MC = \frac{{BC}}{2} = \frac{4}{2} = 2\,\,({\rm{cm)}}\)
Đáp số: a) 4 cm2
b) 6 cm
c) 2 cm
Lời giải
Số tiền lãi nhận được sau một năm là:
20 000 000 × 6 : 100 = 1 200 000 (đồng)
Đáp số: 1 200 000 đồng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập