Chứng minh các phân số sau tối giản với mọi số tự nhiên \(n:\)
a) \[\frac{{n + 1}}{{2n + 3}}.\]
b) \(\frac{{3n - 2}}{{4n - 3}}.\)
Chứng minh các phân số sau tối giản với mọi số tự nhiên \(n:\)
a) \[\frac{{n + 1}}{{2n + 3}}.\]
b) \(\frac{{3n - 2}}{{4n - 3}}.\)
Quảng cáo
Trả lời:
Hướng dẫn giải:
a) Với \(n \in \mathbb{N},\) gọi \[d = \]ƯCLN\[\left( {n + 1,\,2n + 3} \right)\]
Suy ra \[n + 1 \vdots d\] nên \(2\left( {n + 1} \right) \vdots d\) hay \[2n + 2 \vdots d\]
\[2n + 3 \vdots d\]
Do đó \[\left[ {\left( {2n + 3} \right) - \left( {2n + 2} \right)} \right] \vdots d\] hay \[1 \vdots d\]
Suy ra \[d = 1\]
Khi đó ƯCLN\[\left( {n + 1,\,2n + 3} \right) = 1\].
Vậy \[\frac{{n + 1}}{{2n + 3}}\] là phân số sau tối giản với \(n \in \mathbb{N}.\)
b) Với \(n \in \mathbb{N},\) gọi \(d = \)ƯCLN\(\left( {3n - 2,4n - 3} \right)\)
Suy ra \(3n - 2 \vdots d\) nên \(4 \cdot \left( {3n - 2} \right) \vdots d\) hay \(12n - 8 \vdots d\)
\(4n - 3 \vdots d\) nên \(3 \cdot \left( {4n - 3} \right) \vdots d\) hay \(12n - 9 \vdots d\)
Do đó: \(\left[ {\left( {12n - 8} \right) - \left( {12n - 9} \right)} \right] \vdots d\)
\(12n - 8 - 12n + 9 \vdots d\)
\(1 \vdots d\)
Suy ra \(d = 1\)
Khi đó ƯCLN\(\left( {3n - 2,4n - 3} \right) = 1.\)
Vậy phân số \(\frac{{3n - 2}}{{4n - 3}}\) là phân số tối giản với \(n \in \mathbb{N}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải:
Ta có \[\frac{{2025}}{1} = 2025 = \underbrace {1 + 1 + 1... + 1}_{2025\,\,so\,\,hang}\]
Khi đó:
\(B = \frac{{2025}}{1} + \frac{{2024}}{2} + \frac{{2013}}{3} + \ldots + \frac{1}{{2025}}\)
\( = 1 + \left( {\frac{{2024}}{2} + 1} \right) + \left( {\frac{{2013}}{3} + 1} \right) + \ldots + \left( {\frac{1}{{2025}} + 1} \right)\)
\( = 1 + \frac{{2026}}{2} + \frac{{2026}}{3} + ... + \frac{{2026}}{{2025}}\)
\( = \frac{{2026}}{2} + \frac{{2026}}{3} + ... + \frac{{2026}}{{2025}} + \frac{{2026}}{{2026}}\)
\(B = 2026 \cdot \left( {\frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{2025}} + \frac{1}{{2026}}} \right) = 2026A\)
Ta có \(\frac{B}{A} = \frac{{2026A}}{A} = 2026.\)
Vậy \(\frac{B}{A} = 2026.\)
Lời giải
Hướng dẫn giải
Học sinh vẽ đúng sơ đồ mắc vòng như sau:
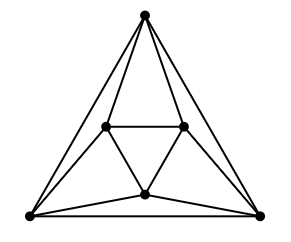
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.