Cô Hồng đầu tư 800 triệu đồng vào hai khoản: Mua trái phiếu doanh nghiệp với lãi suất \(8\% \) một năm và mua trái phiếu chính phủ với lãi suất \(6\% \) một năm. Cuối năm cô Hồng nhận được 54 triệu đồng tiền lãi.

Gọi \(x\;\,\left( {0 < x < 800} \right)\) triệu đồng là số tiền cô Hồng đầu tư vào mua trái phiếu chính phủ.

Hướng dẫn giải

Đáp án: −3

Thay tọa độ điểm \(A\left( { - m; - 3} \right)\) khi \( - 2.\left( { - m} \right) + 3 = - 3\) hay \(2m = - 6\) nên \(m = - 3.\)

Hướng dẫn giải

Đáp án đúng là: a) Đúng.             b) Sai.          c) Đúng.                           d) Đúng.

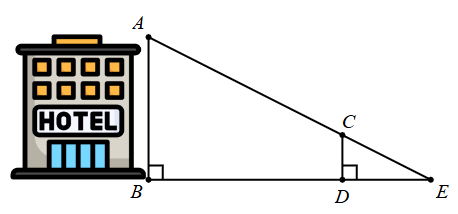
a) Áp dụng định lí Pythagore vào tam giác \(EDC\) vuông tại \(D\), có:

\(E{C^2} = D{C^2} + D{E^2}\,\)(định lí Pythagore)

\(E{C^2} = {3^2} + {4^2}\,\)

\(EC = \sqrt {{3^2} + {4^2}\,} = 5\,\,\left( {\rm{m}} \right)\)

Do đó, ý a) là đúng.

b) Có \(EB \bot DC,\,\,EB \bot AB\) nên \(CD\parallel AB\).

Do đó, xét tam giác \(EAB\) có: \(\frac{{ED}}{{EB}} = \frac{{EC}}{{EA}}\) (hệ quả của định lí Thalès).

Do đó, ý b) là sai.

c) Có \(\frac{{ED}}{{EB}} = \frac{{EC}}{{EA}}\) hay \(\frac{4}{{72}} = \frac{5}{{EA}}\) nên \(AE = \frac{{72 \cdot 5}}{4} = 90\,\,\left( {\rm{m}} \right)\).

Do đó, ý c) là đúng.

d) Xét tam giác \(AEB\) vuông tại \(D\) có: \(A{E^2} = A{B^2} + B{E^2}\) (định lí Pythagore)

Do đó, \(AB = \sqrt {{{90}^2} - {{72}^2}} = 54\,\,\left( {\rm{m}} \right)\).

Vậy chiều cao \(AB\) của tòa nhà là 54 m.

Do đó, ý d) là đúng.