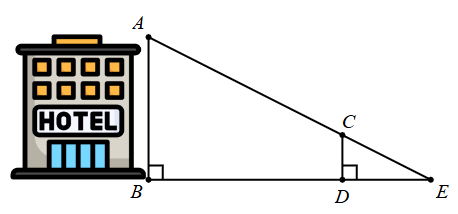
Cho hình vẽ:

Quảng cáo
Trả lời:
Hướng dẫn giải
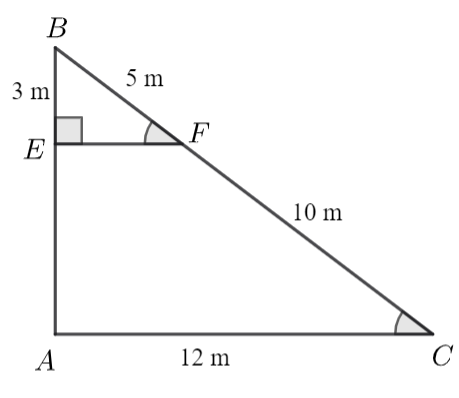
Đáp án đúng là: a) Đúng. b) Đúng. c) Sai. d) Đúng.
a) Vì \(\widehat C = \widehat {BFE},\) mà hai góc này ở vị trí đồng vị nên \(EF\;{\rm{//}}\;AC.\)
Do đó, đáp án a) là đúng.
b) Vì \(EF\;{\rm{//}}\;AC,\) mà \(EF \bot AB\) nên \(AC \bot AB.\) Do đó, tam giác \(ABC\) vuông tại \(A.\)
Do đó, ý b) là đúng.
c) \(\Delta ABC\) có: \(EF\;{\rm{//}}\;AC\) nên theo định lí Thalès ta có: \(\frac{{BE}}{{AB}} = \frac{{BF}}{{BC}} = \frac{{BF}}{{BF + FC}}.\)
Do đó, \(AB = BE:\frac{{BF}}{{BF + FC}} = 3:\frac{5}{{5 + 10}} = 9\;\left( {\rm{m}} \right).\) Vậy \(AB = 9\;{\rm{m}}.\)
Do đó, ý c) là sai.
d) Diện tích \(\Delta ABC\) vuông tại \(A\) là: \(\frac{1}{2}AB \cdot AC = \frac{1}{2} \cdot 9 \cdot 12 = 54\;\left( {{{\rm{m}}^2}} \right).\)
Vậy diện tích tam giác \(ABC\) bằng \(54\;{{\rm{m}}^2}.\)
Do đó, ý d) là đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đúng. b) Sai. c) Đúng. d) Đúng.
a) Áp dụng định lí Pythagore vào tam giác \(EDC\) vuông tại \(D\), có:
\(E{C^2} = D{C^2} + D{E^2}\,\)(định lí Pythagore)
\(E{C^2} = {3^2} + {4^2}\,\)
\(EC = \sqrt {{3^2} + {4^2}\,} = 5\,\,\left( {\rm{m}} \right)\)
Do đó, ý a) là đúng.
b) Có \(EB \bot DC,\,\,EB \bot AB\) nên \(CD\parallel AB\).
Do đó, xét tam giác \(EAB\) có: \(\frac{{ED}}{{EB}} = \frac{{EC}}{{EA}}\) (hệ quả của định lí Thalès).
Do đó, ý b) là sai.
c) Có \(\frac{{ED}}{{EB}} = \frac{{EC}}{{EA}}\) hay \(\frac{4}{{72}} = \frac{5}{{EA}}\) nên \(AE = \frac{{72 \cdot 5}}{4} = 90\,\,\left( {\rm{m}} \right)\).
Do đó, ý c) là đúng.
d) Xét tam giác \(AEB\) vuông tại \(D\) có: \(A{E^2} = A{B^2} + B{E^2}\) (định lí Pythagore)
Do đó, \(AB = \sqrt {{{90}^2} - {{72}^2}} = 54\,\,\left( {\rm{m}} \right)\).
Vậy chiều cao \(AB\) của tòa nhà là 54 m.
Do đó, ý d) là đúng.
Lời giải
Hướng dẫn giải
Đáp án: −3
Thay tọa độ điểm \(A\left( { - m; - 3} \right)\) khi \( - 2.\left( { - m} \right) + 3 = - 3\) hay \(2m = - 6\) nên \(m = - 3.\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.