Cho hình chóp tam giác đều S.ABC cạnh đáy a, đường cao \(SO = 2a\). Gọi M là điểm thuộc đường cao \(AA'\) của tam giác ABC. Xét mặt phẳng \(\left( P \right)\) đi qua M và vuông góc với \(AA'\). Đặt \(AM = x\,\,\left( {\frac{{a\sqrt 3 }}{3} < x < \frac{{a\sqrt 3 }}{2}} \right)\). Giá trị của \(x\) để thiết diện của hình chóp khi cắt bởi \(\left( P \right)\) có diện tích lớn nhất
Cho hình chóp tam giác đều S.ABC cạnh đáy a, đường cao \(SO = 2a\). Gọi M là điểm thuộc đường cao \(AA'\) của tam giác ABC. Xét mặt phẳng \(\left( P \right)\) đi qua M và vuông góc với \(AA'\). Đặt \(AM = x\,\,\left( {\frac{{a\sqrt 3 }}{3} < x < \frac{{a\sqrt 3 }}{2}} \right)\). Giá trị của \(x\) để thiết diện của hình chóp khi cắt bởi \(\left( P \right)\) có diện tích lớn nhất
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
\(x = \frac{{3a\sqrt 3 }}{8}\).
Giải thích
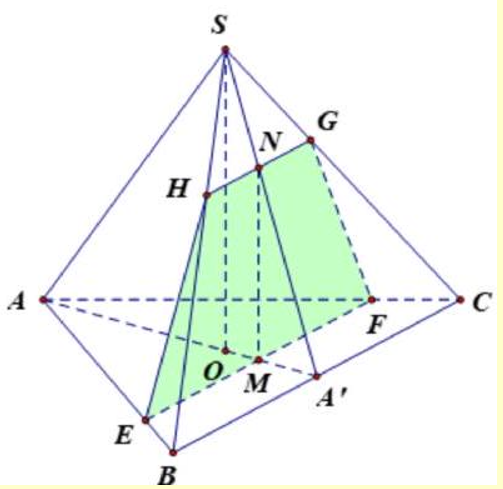
Theo giả thiết \(M\) thuộc \(OA\). Ta có \(SO \bot \left( {ABC} \right) \Rightarrow SO \bot AA'\)
Tam giác \(ABC\) đều nên \(BC \bot AA'\).
Vậy \(\left( P \right)\) qua M song song với SO và BC.
Xét \(\left( P \right)\) và \(\left( {ABC} \right)\) có \(M\) chung. Do \(\left( P \right)//BC\) nên kẻ qua \(M\) đường
thẳng song song với BC cắt \(AB,AC\) tại \(E,F\).
Tương tự kẻ qua M đường thẳng song song với SO cắt \(SA\) tại N , qua N kẻ đường thẳng song song với \(BC\) cắt \(SB,SC\) tại \(H,Q\).
Ta có thiết diện là tứ giác \(EFGH\).
Ta có \(EF//BC//GH,\,\,M,N\) là trung điểm \(EF,GH\) nên \(EFGH\) là
hình thang cân đáy \(HG,EF\). Khi đó \({S_{EFGH}} = \frac{1}{2}\left( {EF + GH} \right)MN\)
Ta có \(MN = \frac{{2x\sqrt 3 }}{3}\) và
\(\frac{{HG}}{{BC}} = \frac{{SN}}{{SA'}} = \frac{{OM}}{{OA'}} \Rightarrow HG = 2\left( {x\sqrt 3 - a} \right)\)
\(\frac{{MN}}{{SO}} = \frac{{MA'}}{{OA'}} \Rightarrow MN = 2\left( {3a - 2x\sqrt 3 } \right)\)
\({S_{EFGH}} = \frac{1}{2}\left( {EF + GH} \right).MN = \frac{2}{3}\left( {4x\sqrt 3 - 3a} \right)\left( {3a - 2x\sqrt 3 } \right)\)
\[{S_{EFGH}} = \frac{1}{3}\left( {4x\sqrt 3 - 3a} \right)(6a - 4x\sqrt 3 )\mathop \le \limits^{{\rm{Cauchy}}} \frac{1}{3}.{\left( {\frac{{3a}}{2}} \right)^2} = \frac{{3{a^2}}}{4}\]
\({S_{EFGH}}\) đạt giá trị lớn nhất bằng \(\frac{{3{a^2}}}{4}\) khi và chỉ khi \(x = \frac{{3a\sqrt 3 }}{8}\).
Vậy giá trị lớn nhất của diện tích thiết diện bằng \(\frac{{3{a^2}}}{4}\) khi \(x = \frac{{3a\sqrt 3 }}{8}\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án
Người mồ côi.
Giải thích
Nhân vật Tấm được xếp vào kiểu nhân vật người mồ côi trong truyện cổ tích.
Lời giải
Đáp án
3003
Giải thích
Số chai nước rửa bát bán cho mỗi vị khách lần lượt là \({x_i},\,\,i = \overline {1,5} \). Khi đó mỗi bộ \({\left( {{x_i}} \right)_{i = \overline {1,5} }}\) là một nghiệm không âm của bất phương trình \({x_1} + {x_2} + \cdots {x_5} \le 10\).
Bất phương trình đưa về dạng tìm số nghiệm không âm của phương trình \({x_1} + {x_2} + \cdots {x_5} + m = 10\)
Vậy có \(C_{15}^5 = 3003\) cách.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập