Âm thanh hay sóng âm là các dao động cơ học (biến đổi vị trí qua lại) của các phân tử, nguyên tử hay các hạt làm nên vật chất và lan truyền trong vật chất như các sóng. Âm thanh, giống như nhiều sóng, được đặc trưng bởi tần số, bước sóng, chu kỳ, biên độ và vận tốc lan truyền (tốc độ âm thanh). Đối với thính giác của người, âm thanh thường là sự dao động, của các phân tử không khí, và lan truyền trong không khí, va đập vào màng nhĩ, làm rung màng nhĩ và kích thích bộ não.

Mức cường độ âm là đại lượng dùng so sánh độ to của một âm với độ to âm chuẩn. Do đặc điểm sinh lí của tai, để âm thanh gây được cảm giác âm, mức cường độ âm phải lớn hơn một giá trị cực tiểu gọi là ngưỡng nghe. Khi mức cường độ âm lên tới giá trị cực đại nào đó, sóng âm gây cho tai cảm giác nhức nhối, đau đớn, gọi là ngưỡng đau.

Tai con người có thể nghe được những âm có tần số nằm trong khoảng

Đáp án

10W/m².

Giải thích

\[{\rm{L}}(\;{\rm{B}}) = \log \frac{{\rm{I}}}{{{{\rm{I}}_0}}} \to {\rm{I}} = {{\rm{I}}_0}{.10^{\rm{L}}} = {10^{ - 12}}{.10^{13}} = 10\,\,{\rm{W/}}{{\rm{m}}^2}\].

Đáp án

32,06 dB.

Giải thích

Gọi A, H, T lần lượt là vị trí thủ môn, huấn luyện viên và trọng tài.

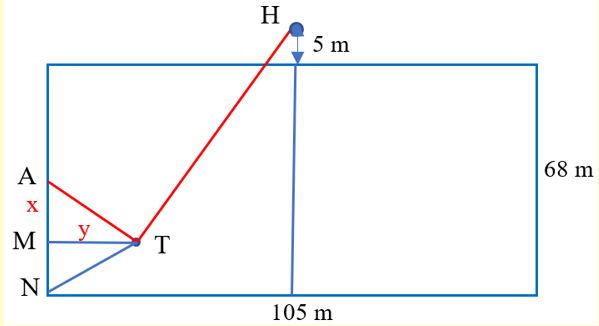
+ Trong ∆ATM có: \({\rm{A}}{{\rm{M}}^2} + {\rm{M}}{{\rm{T}}^2} = {\rm{A}}{{\rm{T}}^2} \to {{\rm{x}}^2} + {{\rm{y}}^2} = 32,{3^2}\) (1)

+ Trong ∆MTN có: \({\rm{M}}{{\rm{N}}^2} + {\rm{M}}{{\rm{T}}^2} = {\rm{N}}{{\rm{T}}^2} \to {({\rm{AN}} - {\rm{AM}})^2} + {\rm{M}}{{\rm{T}}^2} = {\rm{N}}{{\rm{T}}^2}\)

\( \to {\left( {\frac{{68}}{2} - {\rm{x}}} \right)^2} + {{\rm{y}}^2} = 10,{5^2}\) (2)

\( \to 32,{3^2} - {{\rm{x}}^2} = 10,{5^2} - \left( {{{34}^2} - 2.34{\rm{x}} + {{\rm{x}}^2}} \right)\)

\( \to \left\{ {\begin{array}{*{20}{c}}\begin{array}{l}x = 30,72m\\y = 9,98m\end{array}\end{array}} \right.\)

Mà \({\rm{T}}{{\rm{H}}^2} = {\left( {\frac{{105}}{2} - {\rm{y}}} \right)^2} + {\left( {\frac{{68}}{2} + {\rm{x}} + 5} \right)^2}\)

\( \to {\rm{T}}{{\rm{H}}^2} = {\left( {\frac{{105}}{2} - 9,98} \right)^2} + {\left( {\frac{{68}}{2} + 30,72, + 5} \right)^2} \to {\rm{TH}} = 81,66\;{\rm{m}}\)

\[ \to {{\rm{L}}_{\rm{A}}} - {{\rm{L}}_{\rm{H}}} = 10\log \frac{{{\rm{T}}{{\rm{H}}^2}}}{{{\rm{A}}{{\rm{H}}^2}}} = 8,06\;{\rm{dB}}\]

\( \to \;{{\rm{L}}_{\rm{H}}} = {{\rm{L}}_{\rm{A}}} - 8,06 = 40 - 8,06 = 31,94\;{\rm{dB}}{\rm{.}}\)