Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\) \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại 3 điểm có hoành độ lần lượt là \( - 3; - 1;1\) (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng
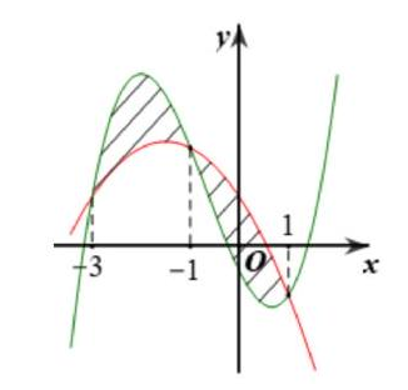
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\) \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại 3 điểm có hoành độ lần lượt là \( - 3; - 1;1\) (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng

Quảng cáo
Trả lời:
Đáp án
4.
Giải thích
Phương trình hoành độ giao điểm của hai đồ thị \(y = f\left( x \right)\) và \(y = g\left( x \right)\) là
\(a{x^3} + b{x^2} + cx - \frac{1}{2} = d{x^2} + ex + 1 \Leftrightarrow a{x^3} + \left( {b - d} \right){x^2} + \left( {c - e} \right)x - \frac{3}{2} = 0.\left( {\rm{*}} \right)\)
Do đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 3; - 1;1\) nên phương trình (\({\rm{*}}\)) có ba nghiệm \(x = - 3;x = - 1;x = 1\). Khi đó ta có hệ phương trình
\(\left\{ {\begin{array}{*{20}{l}}{ - 27a + 9\left( {b - d} \right) - 3\left( {c - e} \right) - \frac{3}{2} = 0}\\{ - a + \left( {b - d} \right) - \left( {c - e} \right) - \frac{3}{2} = 0}\\{a + \left( {b - d} \right) + \left( {c - e} \right) - \frac{3}{2} = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b - d = \frac{3}{2}}\\{a = \frac{1}{2}}\\{c - e = \frac{{ - 1}}{2}}\end{array}} \right.} \right.\).
Suy ra \(f\left( x \right) - g\left( x \right) = \frac{1}{2}{x^3} + \frac{3}{2}{x^2} - \frac{1}{2}x - \frac{3}{2}\).
Vậy hình phẳng giới hạn bởi hai đồ thị hàm số đã cho có diện tích là
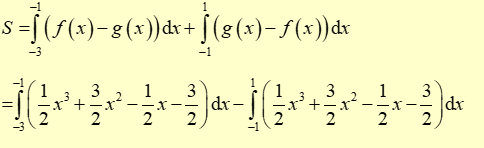
\( = 2 + 2 = 4\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án
providing
Giải thích
commit to V-ing: cam kết làm việc gì
Câu 2
Lời giải
Đáp án
hoàn thành cách mạng dân chủ nhân dân.
Giải thích
Giai đoạn 1945 – 1949, các nước Đông Âu hoàn thành cuộc cách mạng dân chủ nhân dân thông qua việc tiến hành cải cách ruộng đất, ban hành văn bản công nhận các quyền tự do dân chủ, cải thiện và nâng cao đời sống nhân dân. Tháng 10 – 1949, nước Cộng hòa Dân chủ Đức ra đời và sau đó tham gia vào hệ thống các nước xã hội chủ nghĩa Đông Âu. Như vậy, đáp án đúng là hoàn thành cách mạng dân chủ nhân dân.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.