1) Giải phương trình \(2x + 2 = \left( {5 - x} \right)\sqrt {3x - 2} \)

2) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y + 3xy = 9}\\{{x^3} + {y^3} = 9}\end{array}} \right.\)

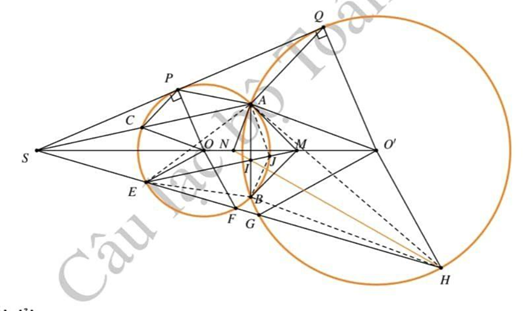
1) Ta thấy OP∥O’Q (do cùng vuông góc với PQ) $\Rightarrow$ \(\frac{{SP}}{{SQ}} = \frac{R}{{R'}}\)

Kẻ O'G'∥OE (G' thuộc SE) $\Rightarrow$ \(\frac{{OE}}{{O'G'}} = \frac{{SO}}{{SO'}} = \frac{R}{{R'}}\) $\Rightarrow$\({\rm{\;}}O'G' = R{\rm{'}}\)$\Rightarrow$ G’ thuộc (O’). Lại có: \(\widehat {OEF} + \widehat {O'HG} < {180^{\rm{o}}}\) nên O’H không song song với OE. Do đó, G’ trùng G $\Rightarrow$OE//O’G (ĐPCM)  

2) Gọi SA∩(O’)=C,A.Tương tự phần a ta cũng chứng minh được OC∥AO’.Theo định lí Thales: \(\frac{{SC}}{{SA}} = \frac{{SO}}{{SO'}} = \frac{{SP}}{{SQ}}\) $\Rightarrow$ PC∥AQ $\Rightarrow$ \(\widehat {SAP} = \widehat {SPC} = \widehat {SQA}\) $\Rightarrow$ \(\Delta {\rm{SAP}}\~\Delta {\rm{SQA}}\) $\Rightarrow$ \(\frac{{SA}}{{SQ}} = \frac{{SP}}{{SA}}\)

$\Rightarrow$ \(S{A^2} = SP.SQ\) (ĐPCM)

3, gọi ME\( \cap \left( O \right) = \left\{ {J,E} \right\}.\;\)Vì tính đối xứng nên ta có MB cũng là tiếp tuyến của (O), ta có \(\Delta MJA\~\Delta MAE\;\left( {g,g} \right){\rm{\;v\`a }}\;\Delta MJB\~\Delta MBE\left( {g.g} \right)\) nên ta được

                     \(\frac{{JA}}{{EA}} = \frac{{MJ}}{{MA}} = \frac{{MJ}}{{MB}} = \frac{{JB}}{{EB}}\)

Từ đó ta thu được \(\frac{{EB}}{{EA}} = \frac{{JB}}{{JA}}\) từ đó để ý rằng \(\Delta IAE\~\Delta IJB\;v\`a \;\Delta IBE\~\Delta IJA\;n\^e n\;ta\;\) được

                             \(\frac{{IA}}{{IB}} = \frac{{IA}}{{IE}}.\frac{{IE}}{{IB}} = \frac{{JA}}{{EB}}.\frac{{EA}}{{JB}} = \frac{{EA}}{{EB}}.\frac{{JA}}{{JB}} = \frac{{E{A^2}}}{{E{B^2}}}\)

Bây giờ ta sẽ chứng minh \(\frac{{EA}}{{EB}} = \frac{{HA}}{{HB}}\). Thật vậy, ta có \(S{P^2}\)= SE . SF và \(S{Q^2} = \) SG . SH.

Do đó \(S{B^2}\) = \(S{A^4} = S{P^2}.S{Q^2} = SE.SF.SG.SH\). Mặt khác, từ câu a ta sẽ có \(\frac{{SE}}{{SF}} = \frac{{SG}}{{SH}}\)  hay SE . SH = SG . SF. Như vậy, ta được \(S{A^2} = S{B^2} = {\left( {SE.SH} \right)^2}\) hay \(S{A^2} = S{B^2} = SE.SH\). Từ đó ta thu được (c.g.c) và  và  (c.g.c). Do vậy,

                                   \(\frac{{EA}}{{HA}} = \frac{{SE}}{{SA}} = \frac{{SE}}{{SB}} = \frac{{EB}}{{HB}}\).

Nói cách khác, ta thu được \(\frac{{EA}}{{EB}} = \frac{{HA}}{{HB}}\). Đến đây, đặt  HN \(.\) AB = I’. Chứng minh tương tự như ý trên ta cũng được \(\frac{{I'A}}{{I'B}} = \frac{{H{A^2}}}{{H{B^2}}}\). Từ đó suy ra \(\frac{{IA}}{{IB}} = \) \(\frac{{I'A}}{{I'B}}\) và dẫn đến I\( \equiv \) I’ . Như vậy, N, I, H thẳng hàng.