Trên bàn có hai túi kẹo: túi thứ nhất có 18 viên kẹo, túi thứ hai có 21 viên kẹo.An và Bình cùng chơi 1 trò chơi như sau: mỗi lượt chơi, 1 bạn sẽ lấy đi 1 viên kẹo từ 1 túi bất kì hoặc là mỗi túi lấy đi 1 viên kẹo. 2 bạn luân phiên thực hiện lượt chơi của mình.Người đầu tiên không thực hiện được lượt chơi của mình là người thua cuộc, người còn lại là người thắng cuộc.Nếu An là người lấy kẹo trước, hãy chỉ ra chiến thuật chơi của An để An là người thắng cuộc.

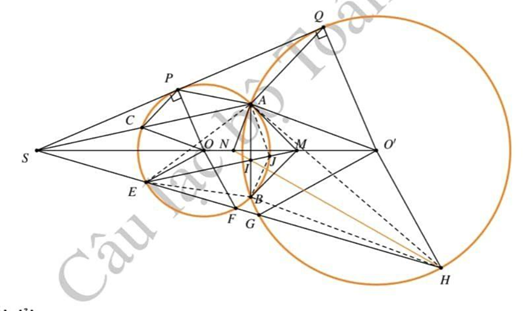
1) Ta thấy OP∥O’Q (do cùng vuông góc với PQ) $\Rightarrow$ \(\frac{{SP}}{{SQ}} = \frac{R}{{R'}}\)

Kẻ O'G'∥OE (G' thuộc SE) $\Rightarrow$ \(\frac{{OE}}{{O'G'}} = \frac{{SO}}{{SO'}} = \frac{R}{{R'}}\) $\Rightarrow$\({\rm{\;}}O'G' = R{\rm{'}}\)$\Rightarrow$ G’ thuộc (O’). Lại có: \(\widehat {OEF} + \widehat {O'HG} < {180^{\rm{o}}}\) nên O’H không song song với OE. Do đó, G’ trùng G $\Rightarrow$OE//O’G (ĐPCM)  

2) Gọi SA∩(O’)=C,A.Tương tự phần a ta cũng chứng minh được OC∥AO’.Theo định lí Thales: \(\frac{{SC}}{{SA}} = \frac{{SO}}{{SO'}} = \frac{{SP}}{{SQ}}\) $\Rightarrow$ PC∥AQ $\Rightarrow$ \(\widehat {SAP} = \widehat {SPC} = \widehat {SQA}\) $\Rightarrow$ \(\Delta {\rm{SAP}}\~\Delta {\rm{SQA}}\) $\Rightarrow$ \(\frac{{SA}}{{SQ}} = \frac{{SP}}{{SA}}\)

$\Rightarrow$ \(S{A^2} = SP.SQ\) (ĐPCM)

3, gọi ME\( \cap \left( O \right) = \left\{ {J,E} \right\}.\;\)Vì tính đối xứng nên ta có MB cũng là tiếp tuyến của (O), ta có \(\Delta MJA\~\Delta MAE\;\left( {g,g} \right){\rm{\;v\`a }}\;\Delta MJB\~\Delta MBE\left( {g.g} \right)\) nên ta được

                     \(\frac{{JA}}{{EA}} = \frac{{MJ}}{{MA}} = \frac{{MJ}}{{MB}} = \frac{{JB}}{{EB}}\)

Từ đó ta thu được \(\frac{{EB}}{{EA}} = \frac{{JB}}{{JA}}\) từ đó để ý rằng \(\Delta IAE\~\Delta IJB\;v\`a \;\Delta IBE\~\Delta IJA\;n\^e n\;ta\;\) được

                             \(\frac{{IA}}{{IB}} = \frac{{IA}}{{IE}}.\frac{{IE}}{{IB}} = \frac{{JA}}{{EB}}.\frac{{EA}}{{JB}} = \frac{{EA}}{{EB}}.\frac{{JA}}{{JB}} = \frac{{E{A^2}}}{{E{B^2}}}\)

Bây giờ ta sẽ chứng minh \(\frac{{EA}}{{EB}} = \frac{{HA}}{{HB}}\). Thật vậy, ta có \(S{P^2}\)= SE . SF và \(S{Q^2} = \) SG . SH.

Do đó \(S{B^2}\) = \(S{A^4} = S{P^2}.S{Q^2} = SE.SF.SG.SH\). Mặt khác, từ câu a ta sẽ có \(\frac{{SE}}{{SF}} = \frac{{SG}}{{SH}}\)  hay SE . SH = SG . SF. Như vậy, ta được \(S{A^2} = S{B^2} = {\left( {SE.SH} \right)^2}\) hay \(S{A^2} = S{B^2} = SE.SH\). Từ đó ta thu được (c.g.c) và  và  (c.g.c). Do vậy,

                                   \(\frac{{EA}}{{HA}} = \frac{{SE}}{{SA}} = \frac{{SE}}{{SB}} = \frac{{EB}}{{HB}}\).

Nói cách khác, ta thu được \(\frac{{EA}}{{EB}} = \frac{{HA}}{{HB}}\). Đến đây, đặt  HN \(.\) AB = I’. Chứng minh tương tự như ý trên ta cũng được \(\frac{{I'A}}{{I'B}} = \frac{{H{A^2}}}{{H{B^2}}}\). Từ đó suy ra \(\frac{{IA}}{{IB}} = \) \(\frac{{I'A}}{{I'B}}\) và dẫn đến I\( \equiv \) I’ . Như vậy, N, I, H thẳng hàng.