(0,5 điểm) Cho một mảnh giấy hình vuông \(ABCD\) cạnh \(6{\rm{ cm}}\). Gọi \(E,\,\,F\) lần lượt là các điểm nằm trên cạnh \(AB,\,\,BC\) sao cho \(AE = 2{\rm{ cm}}\); \(BF = 3{\rm{ cm}}\). Bạn Nam muốn cắt một hình thang \(EFGH\) (hình vẽ) sao cho hình thang đó có diện tích nhỏ nhất. Xác định vị trí của \(G\) (trên \(CD)\) và \(H\) (trên \(AD)\) để bạn Nam có thể thực hiện được mong muốn của mình.
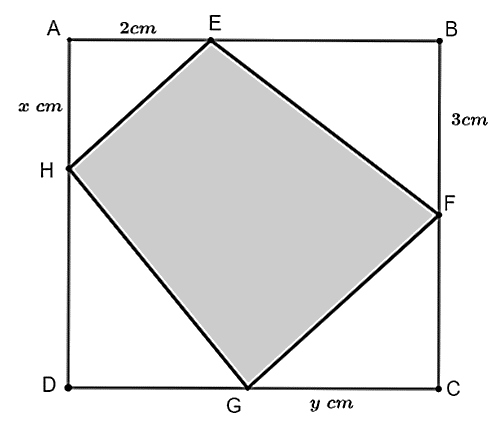
(0,5 điểm) Cho một mảnh giấy hình vuông \(ABCD\) cạnh \(6{\rm{ cm}}\). Gọi \(E,\,\,F\) lần lượt là các điểm nằm trên cạnh \(AB,\,\,BC\) sao cho \(AE = 2{\rm{ cm}}\); \(BF = 3{\rm{ cm}}\). Bạn Nam muốn cắt một hình thang \(EFGH\) (hình vẽ) sao cho hình thang đó có diện tích nhỏ nhất. Xác định vị trí của \(G\) (trên \(CD)\) và \(H\) (trên \(AD)\) để bạn Nam có thể thực hiện được mong muốn của mình.
Câu hỏi trong đề: Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Xét \(\Delta AEH\) và \(\Delta CGF\) có:\(\widehat {EAH} = \widehat {GCF} = 90^\circ \) và \(\widehat {AEH} = \widehat {CGF}\) (dễ dàng chứng minh được từ dữ kiện \(EH\,{\rm{//}}\,GF,\,\,AB\,{\rm{//}}\,CD)\).
Do đó (g.g).
Suy ra \[\frac{{AH}}{{CF}} = \frac{{AE}}{{CG}}\] hay \[\frac{x}{3} = \frac{2}{y}\], do đó \[xy = 6\] và \[y = \frac{6}{x}\].
Diện tích hình vuông \(ABCD\) là: \({S_{ABCD}} = {6^2} = 36{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích tam giác \(BEF\) là: \({S_{BEF}} = \frac{1}{2} \cdot 3 \cdot \left( {6 - 2} \right) = 6{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích hình thang \(EFGH\) là:
\({S_{EFGH}} = {S_{ABCD}} - {S_{BEF}} - {S_{AHE}} - {S_{DHG}} - {S_{CGF}} = 30 - \left( {{S_{AHE}} + {S_{DHG}} + {S_{CGF}}} \right)\)
\( = 30 - \left[ {\frac{1}{2} \cdot 2x + \frac{1}{2}\left( {6 - x} \right)\left( {6 - y} \right) + \frac{1}{2} \cdot 3y} \right]\)
\( = 30 - \left[ {x + \frac{1}{2}\left( {36 - 6y - 6x + xy} \right) + \frac{3}{2}y} \right]\)
\( = 30 - \left[ {x + 18 - 3y - 3x + \frac{1}{2}xy + \frac{3}{2}y} \right]\)
\( = 30 - \left[ { - 2x + 18 - \frac{3}{2}y + \frac{1}{2}xy} \right]\)
\[ = 12 + 2x + \frac{3}{2}y - \frac{1}{2}xy\]
\( = 12 + 2x + \frac{3}{2} \cdot \frac{6}{x} - \frac{1}{2} \cdot 6\) (do \[xy = 6\] và \[y = \frac{6}{x}\]).
\[ = 9 + 2x + \frac{9}{x}.\]
Để \({S_{EFGH}}\) nhỏ nhất thì \(2x + \frac{9}{x}\) đạt giá trị nhỏ nhất.
Áp dụng bất đẳng thức Cauchy, ta có: \(2x + \frac{9}{x} \ge 2\sqrt {2x \cdot \frac{9}{x}} = 6\sqrt 2 \).
Dấu “=” xảy ra khi và chỉ khi \(2x = \frac{9}{x}\) hay \(2{x^2} = 9\), tức là \(x = \frac{{3\sqrt 2 }}{2}.\) Lúc này, \[y = \frac{6}{{\frac{{3\sqrt 2 }}{2}}} = 2\sqrt 2 .\]
Khi đó, \({S_{EFGH}}\) đạt giá trị nhỏ nhất là\({S_{EFGH}} = 9 + 2 \cdot \frac{{3\sqrt 2 }}{2} + \frac{9}{{\frac{{3\sqrt 2 }}{2}}} = 9 + 6\sqrt 2 {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Vậy điểm \(G \in CD\) và \(H \in AD\) sao cho \(CG = 2\sqrt 2 \), \(AH = \frac{{3\sqrt 2 }}{2}\) thì diện tích hình thang \(EFGH\) đạt giá trị nhỏ nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1. a) Điều kiện xác định: \(x \ne 0,x \ne 2\).
Ta có: \(\frac{{x + 2}}{{x - 2}} - \frac{1}{x} = \frac{2}{{x\left( {x - 2} \right)}}\)
\(\frac{{x\left( {x + 2} \right)}}{{x\left( {x - 2} \right)}} - \frac{{x - 2}}{{x\left( {x - 2} \right)}} = \frac{2}{{x\left( {x - 2} \right)}}\)
\(x\left( {x + 2} \right) - \left( {x - 2} \right) = 2\)
\({x^2} + 2x - x + 2 - 2 = 0\)
\({x^2} + x = 0\)
\(x\left( {x + 1} \right) = 0\)
\(x = 0\) hoặc \(x + 1 = 0\)
\(x = 0\) (loại) hoặc \(x = - 1\) (thỏa mãn)
Vậy nghiệm của phương trình là \(x = - 1\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) ⦁ Xét biểu thức \(A = \frac{{\sqrt x + 2}}{{\sqrt x + 3}}\).
Ta có \(\sqrt x + 3 > 0\) với mọi \(x \ge 0\) nên điều kiện xác định của biểu thức \(A\) là \(x \ge 0.\)
⦁ Xét biểu thức \(B = \frac{{\sqrt x + 5}}{{\sqrt x + 1}} + \frac{{7 - \sqrt x }}{{x - 1}}\).
Ta có \(\sqrt x + 1 > 0\) với mọi \(x \ge 0\) nên điều kiện xác định của biểu thức \(B\) là \(x \ge 0,\,\,x \ne 1.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập