a)Cho các số thực \(x;y;z\) thỏa mãn \(0 \le x,\;y,z \le 4\). Chứng minh rằng:
\({x^2}y + {y^2}x + {z^2}x + 16 \ge x{y^2} + y{z^2} + z{x^2}\)
b)Ban đầu trên bảng viết 2023 số thực. Mỗi lần biến đổi số trên bảng là việc thực hiện như sau: Chọn ra hai số \(a,b\) nào đó trên bảng, xóa hai số đi và viết thêm trên bảng số \(\frac{{a + b}}{4}\) . Giả sử ban đầu trên bảng ghi 2023 số 1 và ta thực hiện liên tiếp các biến đổi cho đến khi trên bảng chỉ còn lại một số, chứng minh rằng số đó lớn hơn \(\frac{1}{{{2^{11}}}}\)
a)Cho các số thực \(x;y;z\) thỏa mãn \(0 \le x,\;y,z \le 4\). Chứng minh rằng:
\({x^2}y + {y^2}x + {z^2}x + 16 \ge x{y^2} + y{z^2} + z{x^2}\)
b)Ban đầu trên bảng viết 2023 số thực. Mỗi lần biến đổi số trên bảng là việc thực hiện như sau: Chọn ra hai số \(a,b\) nào đó trên bảng, xóa hai số đi và viết thêm trên bảng số \(\frac{{a + b}}{4}\) . Giả sử ban đầu trên bảng ghi 2023 số 1 và ta thực hiện liên tiếp các biến đổi cho đến khi trên bảng chỉ còn lại một số, chứng minh rằng số đó lớn hơn \(\frac{1}{{{2^{11}}}}\)Quảng cáo
Trả lời:
a) Cho các số thực \(x;y;z\) thỏa mãn \(0 \le x,\;y,z \le 4\). Chứng minh rằng:
\({x^2}y + {y^2}x + {z^2}x + 16 \ge x{y^2} + y{z^2} + z{x^2}\)
Ta có:
\({x^2}y + {y^2}z + {z^2}x + 16 \ge x{y^2} + y{z^2} + z{x^2}\)
\( \Leftrightarrow {x^2}y + {y^2}z + {z^2}x + 16 - x{y^2} - y{z^2} - z{x^2} \ge 0\)
\( \Leftrightarrow )x - y)\left( {x - z} \right)\left( {y - z} \right) + 16 \ge 0\)
Ta có bất đẳng thức: \(ab \ge - \frac{1}{4}{\left( {a - b} \right)^2},\;\forall a,b \in \mathbb{R}\)
và \(ab \le \frac{{{{\left( {a + b} \right)}^2}}}{4}\;,\forall a,b \in \mathbb{R}\)
Trường hợp 1: Nếu \(x \ge y\) ta có \(\left( {x - z} \right)\left( {y - z} \right) \ge - \frac{1}{4}{\left( {x - y} \right)^2}\)
nên \(\left( {x - y} \right)\left( {x - z} \right)\left( {y - z} \right) + 16 \ge - \frac{1}{4}{\left( {x - y} \right)^3} + 16 \ge - \frac{1}{4}{4^3} + 16 \ge 0\)
Trường hợp 2: Nếu \(y > x\) ta xét
Trường hợp 2.1: Nếu \(y \ge z\), ta có \(\left( {x - y} \right)\left( {x - z} \right) \ge - \frac{1}{4}{\left( {y - z} \right)^2}\)
nên \(\left( {x - y} \right)\left( {x - z} \right)\left( {y - z} \right) + 16 \ge - \frac{1}{4}{\left( {y - z} \right)^3} + 16 \ge - \frac{1}{4}{4^3} + 16 \mp 0\)
Trường hợp 2.2: Nếu \(y < z\), ta có: \(\left( {x - y} \right)\left( {x - z} \right)\left( {y - z} \right) + 16 = \left( {y - z} \right)\left( {x - z} \right)\left( {x - y} \right) = 16\)
Kết hợp với \(\left( {y - x} \right)\left( {z - y} \right) \le - \frac{1}{4}{\left( {z - x} \right)^2}\;v\`a \;x < y < z\)
Ta được: \(\left( {y - x} \right)\left( {x - z} \right)\left( {z - y} \right) + 16 \ge \frac{1}{4}{\left( {z - x} \right)^2}\left( {x - z} \right) + 16 = - \frac{1}{4}{\left( {z - x} \right)^3} + 16 \ge 0\)
Vậy với mọi trường hợp thì \(\left( {x - y} \right)\left( {x - z} \right)\left( {y - z} \right) + 16 \ge 0\) hay
\({x^2}y + {y^2}z + {z^2}x + 16 \ge x{y^2} + y{z^2} + z{x^2}\)
b) Ban đầu trên bảng viết 2023 số thực. Mỗi lần biến đổi số trên bảng là việc thực hiện như sau: Chọn ra hai số \(a,b\) nào đó trên bảng, xóa hai số đi và viết thêm trên bảng số \(\frac{{a + b}}{4}\) . Giả sử ban đầu trên bảng ghi 2023 số 1 và ta thực hiện liên tiếp các biến đổi cho đến khi trên bảng chỉ còn lại một số, chứng minh rằng số đó lớn hơn \(\frac{1}{{{2^{11}}}}\)
Trước hết ta thấy trên bảng luôn là các số dương. Thật vậy, ta sử dụng quy nạp. Ban đầu có 2023 số 1 đều là số dương. Giả sử sau lần biến đổi thứ i, trên bảng đều là số dương. Đến bước biến đổi thứ i + 1: Ta chọn hai số \(a,\;b\) trên bảng (theo giả thiết quy nạp thì \(a,b > 0\), ta xóa hai số đó đi và viết thêm số \(\frac{{a + b}}{4}\) cùng là số dương. Vậy, mỗi số được viết trên bảng luôn là các số dương.
Gọi \({T_i}\) là tổng các nghịch đảo của các số thực còn lại trên bảng sau bước biến đổi thứ i (\({T_0}\) là tổng nghịch đảo của các số thực trên bảng khi chưa thực hiện bược biến đổi nào) thì:
Ở bước thứ i ta có tổng \({T_i}\). Đến bước thứ i + 1 ta xóa đi hai số \(a,b\) và viết lên bảng số \(\frac{{a + b}}{4}\) thì ta có tổng \({T_{i + 1}}\) và:
\({T_{i + 1}} = {{\rm{T}}_{\rm{i}}} - \left( {\frac{1}{a} + \frac{1}{b}} \right) + \frac{1}{{\frac{{a + b}}{4}}}\)
Suy ra \({T_{i + 1}} - {{\rm{T}}_{\rm{i}}} = - \frac{{{{\left( {a - b} \right)}^2}}}{{ab\left( {a + b} \right)}} \le 0\) (Vì \(a,b\) đều lớn hơn 0)
Như vậy: \({T_{2022}} \le {T_{2021}} \le \ldots \le {T_0}\)
Ban đầu, ta có trên bảng 2023 số 1 nên \({T_0} = 2023\). Sau 2022 bước thì ta được trên bảng một số x nào đó. Khi đó \({T_{2022}} = \frac{1}{x} \le {T_0} = 2023\)
Vì ban đầu các số trên bảng đều là 1, các bước xóa bỏ và thay thể đều chỉ sử dụng phép toán cộng và chia, nên sau mỗi bước thay số trên bảng luôn còn lại tất cả các số đều là các số dương. Như vậy \(x > 0\).
Từ đó ta có \(x \ge \frac{1}{{2023}} \ge \frac{1}{{2048}} \ge \frac{1}{{{2^{11}}}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
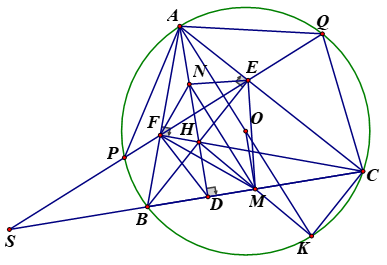
a) Tứ giác AOMN là hình bình hành.
Kẻ đường kính AK (K nằm trên đường tròn (O)). Khi đó \(AC \bot CK;BK \bot AB\).
Dễ dàng suy ra \(BK//CH\) và \(CK//BH\) (cùng vuông góc với một đường thẳng).
Từ đó suy ra BHCK là hình bình hành. Vì M là trung điểm BC nên \(M \in HK\) và \(MH = MK\).
Tam giác AHK có M và N lần lượt là trung điểm của HK và AH nên MN là đường trung bình của . Suy ra \(MN//AO\) và \(MN = \frac{1}{2}AK = AO.\)
Vậy AOMN là hình bình hành.
\(b)\;A{P^2} = A{Q^2} = AE.AC.\)
Tam giác AFH vuông tại F suy ra \(FN = NH\). Tương tự, vuông tại E nên \(NE = NH\). Như vậy \(NF = NE\;\;\;\left( 1 \right)\).
Lại có và lần lượt vuông tại F và E, có các đường trung tuyến lần lượt là MF và ME. Do đó \(MF = ME = \frac{1}{2}BC\;\;\;\left( 2 \right)\).
Từ (1) và (2) suy ra MN là trung trực của EF. Suy ra \(EF \bot MN\;\;\;\left( 3 \right)\).
Lại có \(MN//AO\), kết hợp với (3) suy ra \(AO \bot EF\) hay \(AO \bot PQ\). Suy ra A là điểm chính giữa cung PAQ, suy ra \(AP = AQ\) hay cung AQ bằng cung AP.
Mặt khác, \(\widehat {AQP} = \widehat {APQ} = \widehat {ACQ}\) (các góc nội tiếp chắn các cung bằng nhau). Nên .
Suy ra \(\frac{{AE}}{{AQ}} = \frac{{AQ}}{{AC}} \Rightarrow AE.AC = A{Q^2}\)
Vậy \(A{P^2} = A{Q^2} = AE.AC\)
c) Tứ giác DMEF nội tiếp và \(\frac{{FP}}{{PS}} = \frac{{QE}}{{ES}}\)
Tứ giác BFEC nội tiếp suy ra \(\widehat {AEF} = \widehat {ABC}.\)
Tam giác EMC cân tại M nên \(\widehat {MEC} = \widehat {ACB}\).
Suy ra \(\widehat {FEM} = {180^0} - \widehat {AEF} - \widehat {MEC} = {180^0} - \widehat {ABC} - \widehat {ACB} = \widehat {BAC}.\)
Tứ giác DFAC nội tiếp nên \(\widehat {FDM} + \widehat {BAC} = {180^0}\). Suy ra \(\widehat {FEM} = \widehat {FDM} = {180^0}\)
Vậy tứ giác DMEF là tứ giác nội tiếp.
Hai tam giác SDF và SEM có:
\(\widehat {SDF} = \widehat {SEM};\) chung \(\widehat {DSF}\) nên chúng đồng dạng
Suy ra \(\frac{{SD}}{{SF}} = \frac{{SE}}{{SM}}\) hay \(SD.SM = SE.SF\).
Từ tứ giác BFEC nội tiếp, ta cũng suy ra \(SE.SF = SB.SC\), tứ giác BCQP nội tiếp ta cũng có \(SB.SQ = SP.SQ\).
Suy ra \(SP.SQ = SE.SF\) \( \Rightarrow \frac{{SF}}{{SP}} = \frac{{SQ}}{{SE}}\)
Vậy \(\frac{{SF}}{{SP}} - 1 = \frac{{SQ}}{{SE}} - 1\) hay \(\frac{{SF - SP}}{{SP}} = \frac{{SQ - SE}}{{SE}} \Rightarrow \frac{{PF}}{{PS}} = \frac{{EQ}}{{SE}}\)
Lời giải
a) Cho \(x,\;y,\;z\) là ba số thực khác 0 thỏa mãn: \(x + \frac{y}{2} + \frac{z}{3}\) =1 và \(\frac{1}{x} + \frac{2}{y} + \frac{3}{z}\) = 0. Chứng minh rằng: \({x^2} + \frac{{{y^2}}}{4} + \frac{{{z^2}}}{9}\) =1
Bằng cách quy đồng mẫu số ta được:
\(\frac{1}{x} + \frac{2}{y} + \frac{3}{z} \Rightarrow yz + 2zx + 3xy = 0\;\;\;\left( 1 \right)\)
Lại có:
\({\left( {x + \frac{y}{2} + \frac{z}{3}} \right)^2} = {x^2} + \frac{{{y^2}}}{4} + \frac{{{z^2}}}{9} + 2\left( {\frac{{xy}}{2} + \frac{{yz}}{6} + \frac{{zx}}{3}} \right)\)
\(\; = {x^2} + \frac{{{y^2}}}{4} + \frac{{{z^2}}}{9} + \frac{{3xy + yz + 2xz}}{3} = 1\;\;\;\left( 2 \right)\)
Kết hợp (1) và (2) ta được: \({x^2} + \frac{{{y^2}}}{4} + \frac{{{z^2}}}{9}\) =1
b) Cho \(f\left( n \right) = \) \(\frac{2}{{\sqrt {2n + 1} + \sqrt {2n - 1} }}\) với n là số nguyên dương. Tính giá trị của biểu thức:
\(S = f\left( 1 \right) + f\left( 2 \right) + f\left( 3 \right) + \ldots + f\left( {40} \right)\)
Biến đổi:
\(f\left( n \right) = \frac{2}{{\sqrt {2n + 1} + \sqrt {2n - 1} }}\)
\( = \frac{{2\left( {\sqrt {2n + 1} - \sqrt {2n - 1} } \right)}}{{\left( {2n + 1} \right) - \left( {2n - 1} \right)}}\;(\;do\;\sqrt {2n + 1} - \sqrt {2n - 1} \ne 0\)
\( = \sqrt {2n + 1} - \sqrt {2n - 1} \)
Như vậy:
\(S = f\left( 1 \right) + f\left( 2 \right) + f\left( 3 \right) + \ldots + f\left( {40} \right)\)
\( = \left( {\sqrt 3 - \sqrt 1 } \right) + \left( {\sqrt 5 - \sqrt 3 } \right) + \left( {\sqrt 7 - \sqrt 3 } \right) + \ldots + \left( {\sqrt {81} - \sqrt {79} } \right)\)
\( = \sqrt {81} - \sqrt 1 = 9 - 1 = 8\)
Vậy giá trị \(S = 8\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.