(1,5 điểm) Trong một buổi luyện tập, một tàu ngầm ở trên mặt biển bắt đầu lặn xuống và di chuyển theo một đường thẳng tạo với mặt nước một góc \(21^\circ .\)
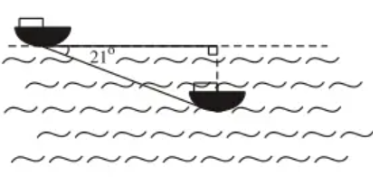
a) Khi tàu chuyển động theo hướng đó và đi được \(250{\rm{ m}}\)thì tàu ở độ sâu bao nhiêu so với mặt nước (kết quả làm tròn đến hàng phần mười)?
(1,5 điểm) Trong một buổi luyện tập, một tàu ngầm ở trên mặt biển bắt đầu lặn xuống và di chuyển theo một đường thẳng tạo với mặt nước một góc \(21^\circ .\)

a) Khi tàu chuyển động theo hướng đó và đi được \(250{\rm{ m}}\)thì tàu ở độ sâu bao nhiêu so với mặt nước (kết quả làm tròn đến hàng phần mười)?
Quảng cáo
Trả lời:
Hướng dẫn giải
Giả sử hình ảnh chiếc tàu trong bài toán được mô tả bởi hình vẽ sau:
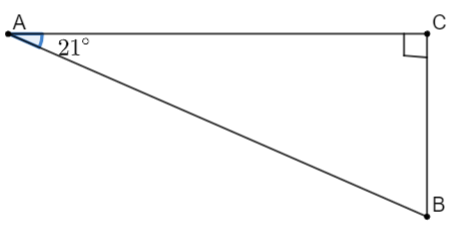
a) Xét tam giác \(ABC\) vuông tại \(C\) ta có:
\(CB = AB.\sin A = 250.\sin 21^\circ \approx 89,6{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\)
Vậy tàu đi được \(250{\rm{ m}}\)thì tàu ở độ sâu khoảng \(89,6{\rm{ m}}{\rm{.}}\)
Câu hỏi cùng đoạn
Câu 2:
b) Giả sử tốc độ trung bình của tàu là \(9{\rm{ km/h}}\) thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu \(200{\rm{ m,}}\) tức là cách mặt biển \(200{\rm{ m}}\) (kết quả làm tròn đến hàng phần trăm)?
b) Giả sử tốc độ trung bình của tàu là \(9{\rm{ km/h}}\) thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu \(200{\rm{ m,}}\) tức là cách mặt biển \(200{\rm{ m}}\) (kết quả làm tròn đến hàng phần trăm)?
b) Đổi \(9\) km/h \( = 2,5\) m/s.
Gọi \(t\) (s) là thời gian để tàu đi được độ sâu \(200{\rm{ m}}{\rm{.}}\)
Quãng đường tàu đi được trong thời gian \(t\) là: \(AB = {S_{AB}} = 2,5t{\rm{ }}\left( {\rm{m}} \right).\)
Xét tam giác \(ABC\) vuông tại \(C\), ta có: \(\sin A = \frac{{BC}}{{AB}}\).
Suy ra \(AB = \frac{{CB}}{{\sin A}}\) hay \(2,5t = \frac{{200}}{{\sin 21^\circ }}\), suy ra \(t = \frac{{200}}{{2,5.\sin 21^\circ }} \approx 223,23{\rm{ }}\left( {\rm{s}} \right)\).
Đổi \(223,23{\rm{ s}} \approx 3\) phút \(43\) giây.
Vậy sau khoảng \({\rm{3}}\) phút \(43\) giây thì tàu ở độ sâu \(200{\rm{ m}}{\rm{.}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1. a) Điều kiện xác định: \(x \ne 0,x \ne 2\).
Ta có: \(\frac{{x + 2}}{{x - 2}} - \frac{1}{x} = \frac{2}{{x\left( {x - 2} \right)}}\)
\(\frac{{x\left( {x + 2} \right)}}{{x\left( {x - 2} \right)}} - \frac{{x - 2}}{{x\left( {x - 2} \right)}} = \frac{2}{{x\left( {x - 2} \right)}}\)
\(x\left( {x + 2} \right) - \left( {x - 2} \right) = 2\)
\({x^2} + 2x - x + 2 - 2 = 0\)
\({x^2} + x = 0\)
\(x\left( {x + 1} \right) = 0\)
\(x = 0\) hoặc \(x + 1 = 0\)
\(x = 0\) (loại) hoặc \(x = - 1\) (thỏa mãn)
Vậy nghiệm của phương trình là \(x = - 1\).
Lời giải
a) ⦁ Xét biểu thức \[A = \frac{{\sqrt x - 2}}{{\sqrt x + 7}}\].
Với \(x \ge 0,\) ta luôn có \(\sqrt x + 7 > 0.\)
Điều kiện xác định của biểu thức \(A\) là \(x \ge 0.\)
⦁ Xét biểu thức \(B = \frac{x}{{x - 4}} - \frac{1}{{2 - \sqrt x }} + \frac{1}{{\sqrt x + 2}}\).
Với \(x \ge 0,\) ta có \[x - 4 = \left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right).\]
Điều kiện xác định của biểu thức \(B\) là \(x \ge 0,\,\,x - 4 \ne 0\) tức là \(x \ge 0,\,\,x \ne 4.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.