a) Giải hệ phương trình \[\left\{ \begin{array}{l}2\sqrt {x - 3y} = 16 - 3x + 9y\\2\sqrt {x - 3} + \sqrt {y + 3} = 5y + 1\end{array} \right.{\rm{ }}\left( {x,y \in \mathbb{R}} \right).\]
b) Viết lên trên bảng 2023 số: \[1;\frac{1}{2};\frac{1}{3}; \cdots ;\frac{1}{{2022}};\frac{1}{{2023}}\]. Mỗi bước ta xoá đi 2 số \(x,y\) bất kì trên bảng rồi viết lên bảng số \[\frac{{xy}}{{x + y + 1}}\] (các số còn lại trên bảng giữ nguyên). Thực hiện liên tục thao tác trên cho đến khi trên bảng chỉ còn lại đúng một số. Hỏi số đó bằng bao nhiêu?
a) Giải hệ phương trình \[\left\{ \begin{array}{l}2\sqrt {x - 3y} = 16 - 3x + 9y\\2\sqrt {x - 3} + \sqrt {y + 3} = 5y + 1\end{array} \right.{\rm{ }}\left( {x,y \in \mathbb{R}} \right).\]
b) Viết lên trên bảng 2023 số: \[1;\frac{1}{2};\frac{1}{3}; \cdots ;\frac{1}{{2022}};\frac{1}{{2023}}\]. Mỗi bước ta xoá đi 2 số \(x,y\) bất kì trên bảng rồi viết lên bảng số \[\frac{{xy}}{{x + y + 1}}\] (các số còn lại trên bảng giữ nguyên). Thực hiện liên tục thao tác trên cho đến khi trên bảng chỉ còn lại đúng một số. Hỏi số đó bằng bao nhiêu?
Quảng cáo
Trả lời:
a)Điều kiện: \[x - 3y \ge 0;x \ge 3;y \ge - 3.\]
Ta có:
\[\begin{array}{l}(1) \Leftrightarrow 3(x - 3y) + 2\sqrt {x - 3y} - 16 = 0 \Leftrightarrow \left( {\sqrt {x - 3y} - 2} \right)\left( {3\sqrt {x - 3y} + 8} \right) = 0 \Leftrightarrow \sqrt {x - 3y} = 2\\ \Leftrightarrow x = 4 + 3y.\end{array}\]
Thế \[x = 3y + 4\] vào phương trình (2) ta được \[2\sqrt {3y + 1} + \sqrt {y + 3} = 5y + 1 \Leftrightarrow 2\left( {\sqrt {3y + 1} - 2} \right) + \left( {\sqrt {y + 3} - 2} \right) = 5y + 1 - 6\]
\[ \Leftrightarrow 2\frac{{3\left( {y - 1} \right)}}{{\sqrt {3y + 1} + 2}} + \frac{{y - 1}}{{\sqrt {y + 3} + 2}} - 5\left( {y - 1} \right) = 0 \Leftrightarrow \left( {y - 1} \right)\left( {\frac{6}{{\sqrt {3y + 1} + 2}} + \frac{1}{{\sqrt {y + 3} + 2}} - 5} \right) = 0{\rm{ }}\left( * \right)\]
Nhận thấy \(\frac{6}{{\sqrt {3y + 1} + 2}} + \frac{1}{{\sqrt {y + 3} + 2}} - 5 < 3 + \frac{1}{2} - 5 < 0\) với mọi \(y \ge - 3.\)
Do đó \(\left( * \right)\) có nghiệm duy nhất \(y = 1\)(thỏa mãn).
Với \[y = 1\] ta được \[x = 7\](thỏa mãn).
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {7;1} \right).\)
b)Đặt \[z = \frac{{xy}}{{x + y + 1}} \Rightarrow \frac{1}{z} = \frac{1}{x} + \frac{1}{y} + \frac{1}{{xy}} \Rightarrow \frac{1}{z} + 1 = \left( {\frac{1}{x} + 1} \right)\left( {\frac{1}{y} + 1} \right){\rm{ }}\left( 1 \right).\]
Với mỗi tập các số dương \[\left\{ {{x_1};{x_2};...{x_n}} \right\}\]tùy ý, xét biểu thức:
\[P\left( {{x_1};{x_2};...{x_n}} \right) = \left( {\frac{1}{{{x_1}}} + 1} \right)\left( {\frac{1}{{{x_2}}} + 1} \right)....\left( {\frac{1}{{{x_n}}} + 1} \right).\]
Từ \(\left( 1 \right)\) suy ra mỗi lần xóa đi 2 số bất kì \(x,y\) rồi viết lên bảng số \[\frac{{xy}}{{x + y + 1}}\]các số còn lại trên bảng giữ nguyên thì giá trị biểu thức \(P\) của các số trên bảng không đổi.
Gọi số cuối cùng là a \[ \Rightarrow P(a) = P\left( {\frac{1}{1};\frac{1}{2};\frac{1}{3};...;\frac{1}{{2022}};\frac{1}{{2023}}} \right)\]
\[ \Rightarrow \frac{1}{a} + 1 = \left( {\frac{1}{1} + 1} \right).\left( {\frac{1}{{\frac{1}{2}}} + 1} \right)...\left( {\frac{1}{{\frac{1}{{2022}}}} + 1} \right).\left( {\frac{1}{{\frac{1}{{2023}}}} + 1} \right) = 2024! \Rightarrow a = \frac{1}{{2024! - 1}}.\]
Vậy số còn lại trên bảng là \[a = \frac{1}{{2024! - 1}}.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)Vì \[\left( {{x^2} - x - 1} \right)\left( {{y^2} + xy - 6} \right) = 2x + 1\] nên \(\left( {2x + 1} \right)\, \vdots \,\left( {{x^2} - x - 1} \right)\)
\( \Rightarrow \left( {2x + 1} \right)\left( {2x - 3} \right)\, \vdots \,\left( {{x^2} - x - 1} \right)\)
\( \Rightarrow \left( {4{x^2} - 4x - 3} \right)\, \vdots \,\left( {{x^2} - x - 1} \right)\)
\( \Rightarrow \left[ {4\left( {{x^2} - x - 1} \right) + 1} \right]\, \vdots \,\left( {{x^2} - x - 1} \right)\)
\( \Rightarrow 1\, \vdots \,\left( {{x^2} - x + 1} \right)\)
\( \Rightarrow \left( {{x^2} - x - 1} \right) \in \left\{ { - 1\,;1} \right\}\)
\( \Rightarrow x \in \left\{ {\,0\,;\,1\,;\, - 1;2} \right\}\), mà \(x\)nguyên dương \( \Rightarrow x \in \left\{ {\,1\,;\,2} \right\}.\)
Với \(x = 1\), ta có phương trình: \({y^2} + y - 9 = - 3\)\( \Leftrightarrow y = 2\) hoặc \(y = - 3 < 0\)(không thỏa mãn)
Với \(x = 2\), ta có phương trình: \({y^2} + 2y - 9 = 5 \Leftrightarrow {y^2} + 2y - 14 = 0\) (loại do phương trình có 2 nghiệm không nguyên).
Thử lại \(\left( {x;y} \right) = \left( {1;2} \right)\) thỏa mãn phương trình đã cho.
Vậy cặp số nguyên dương \(\left( {x;y} \right)\)cần tìm là \(\left( {1;2} \right)\).
b)- Với \(n = 1 \Rightarrow {3^n} + {7^n} = 3 + 7 = 10\cancel{ \vdots }11\) (không thỏa mãn).
- Với \(n = 3 \Rightarrow {3^n} + {7^n} = {3^3} + {7^3} = 370\cancel{ \vdots }11\) (không thỏa mãn).
- Với \(n = 5 \Rightarrow {3^n} + {7^n} = {3^5} + {7^5} = 17050 \vdots 11\) (thỏa mãn).
Suy ra \(n \ge 5\). Giả sử \(n = 5k + r{\rm{ }}\left( {0 \le r \le 4} \right)\).
Ta có \({3^{5k + r}} + {7^{5k + r}} = {\left( {{3^5}} \right)^k}{.3^r} + {\left( {{7^5}} \right)^k}{.7^r} \equiv {3^r} + {7^r}.{\left( { - 1} \right)^k} \vdots 11\) với \(r = 0,1,2,3,4\).
- Khi \(r = 0\)\( \Rightarrow {3^r} + {7^r}.{\left( { - 1} \right)^k} = 1 + {\left( { - 1} \right)^k} \vdots 11\) xảy ra khi \(k\) lẻ.
- Khi \(r = 1\)\( \Rightarrow {3^r} + {7^r}.{\left( { - 1} \right)^k} = 3 + 7.{\left( { - 1} \right)^k}\cancel{ \vdots }11\) với mọi \(k\).
- Khi \(r = 2\)\( \Rightarrow {3^r} + {7^r}.{\left( { - 1} \right)^k} = {3^2} + {7^2}.{\left( { - 1} \right)^k}\cancel{ \vdots }11\) với mọi \(k\).
- Khi \(r = 3\)\( \Rightarrow {3^r} + {7^r}.{\left( { - 1} \right)^k} = {3^3} + {7^3}.{\left( { - 1} \right)^k}\cancel{ \vdots }11\) với mọi \(k\).
- Khi với mọi
Vậy (![]() lẻ).
lẻ).
Khi đó
Vậy \({2^n} + {6^n} + {2023^n}\) chia \(11\) có số dư là \(8.\)
Lời giải
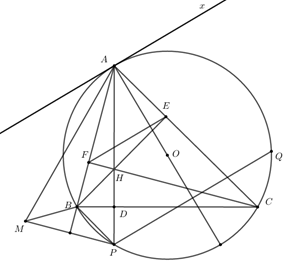
a) Vì \(M\) là điểm đối xứng với \(P\) qua \(AB\) nên \(\widehat {AMB} = \widehat {APB}\)
Mà \(\widehat {APB} = \widehat {ACB}\)(góc nội tiếp cùng chắn cung ).
Mặt khác: \(\widehat {ACB} = \widehat {AHE}\)(vì tứ giác \(AEHF\) nội tiếp)
Ta được\(\widehat {AMB} = \widehat {AHE}\) do đó tứ giác \(AHBM\) nội tiếp.
b) Kẻ tiếp tuyến \[Ax\] của đường tròn \(\left( O \right)\). Ta có \(\widehat {xAC} = \widehat {ABC}\)
\[\widehat {ABC} = \widehat {AEF}\](vì tứ giác \(BCEF\) nội tiếp)
\( \Rightarrow \widehat {xAC} = \widehat {AEF}\)
\[ \Rightarrow Ax,EF\] song song. Mà \[OA \bot Ax\]\( \Rightarrow OA \bot EF\)
Theo giả thiết \(PQ,EF\) song song với nhau nên\(PQ \bot OA.\) Do đó theo định lý đường kính, dây cung ta được \(Q\) đối xứng với \(P\) qua \(OA\).
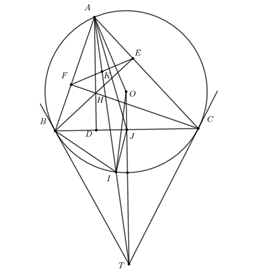
c)Tiếp tuyến tại \(B,C\) cắt nhau ở \(T\). Gọi \(I = AT \cap \left( O \right)\). Lấy \(J\) là trung điểm của \(BC\)\( \Rightarrow O,J,T\) thẳng hàng.
Có \(TI.TA = T{B^2} = TJ.TO\) \( \Rightarrow \) tứ giác \(AOJI\) nội tiếp.
\( \Rightarrow \widehat {IJT} = \widehat {OAI} = \widehat {OIA} = \widehat {OJA} \Rightarrow \widehat {AJB} = \widehat {BJI}\)\( \Rightarrow JB\) là phân giác của góc \(\widehat {AJI}\)
Xét \(\widehat {AJC} = 180^\circ - \widehat {AJB} = 180^\circ - \frac{1}{2}\widehat {AJI} = 180^\circ - \frac{1}{2}\widehat {AOI} = 180^\circ - \widehat {ACI} = \widehat {ABI}\)
Xét \(\Delta AJC\) và \(\Delta ABI\)có: \(\widehat {AJC} = \widehat {ABI}\); \(\widehat {ACJ} = \widehat {AIB}.\)
\( \Rightarrow \widehat {JAC} = \widehat {BAI}{\rm{ }}\left( 1 \right)\)
Mặt khác \(\Delta AEF\) và \(\Delta ABC\) đồng dạng có hai đường trung tuyến tương ứng là \(AK,AJ\)
\( \Rightarrow \widehat {KAF} = \widehat {JAC}{\rm{ }}\left( 2 \right)\)
Từ \((1),(2) \Rightarrow \widehat {BAI} = \widehat {FAK} \Rightarrow I \in AK\)\( \Rightarrow A,I,K\) thẳng hàng. Vậy đường thẳng\(AK\) và hai tiếp tuyến của \(\left( O \right)\) tại \(B\) và \(C\) đồng quy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.