Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{{x^2} + xy - 2{y^2} = x + 2y}\\{{x^3} + 2{x^2}y = {x^2} + {y^2} - 1}\end{array}} \right.\)

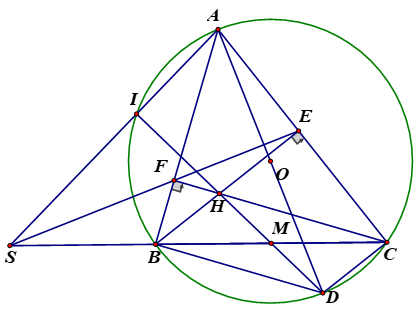
a) Chứng minh rằng tứ giác AFHE là tứ giác nội tiếp.

Do \(BE \bot AC;CF \bot AB \Rightarrow \widehat {AEB} = \widehat {AFC} = {90^0}\)

Xét tứ giác AEHF có: \(\widehat {AEH} + \widehat {AFH} = {90^0} + {90^0} = {180^0}\)

\( \Rightarrow \) Tứ giác AEHF nội tiếp đường tròn.

b) Chứng minh \(SF.SE = SI.SA\) và \(HI \bot SA\).

Xét tứ giác BFEC có : \(\widehat {BFC} = \widehat {BEC} = {90^0}\)

Mà 2 góc này cùng nhìn cạnh BC

\( \Rightarrow \) Tứ giác BFEC nội tiếp đường tròn.

\( \Rightarrow \widehat {FEB} = \widehat {FCB}\) (hai góc nội tiếp cùng chắn cung BF)

Xét tam giác SEB và tam giác SCF có:

\(\widehat {ESC}\;\) là góc chung

                                                                       \(\widehat {SEB} = \widehat {SCF}\)

 (g-g)

           \( \Rightarrow \frac{{SE}}{{SC}} = \frac{{SB}}{{SF}} \Rightarrow SE.SF = SB.SC\;\;\left( 1 \right)\)

Xét tam giác SAB và tam giác SCI có:

          \(\widehat {ASC}\;\)chung

\(\widehat {SAB} = \widehat {SCI} = \frac{1}{2}\;\)số đo cung IB (góc nội tiếp)

 (g-g)

             \( \Rightarrow \frac{{SA}}{{SC}} = \frac{{SB}}{{SI}} \Rightarrow SA.SI = SB.SC\;\;\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow SE.SF = SA.SI\; \Rightarrow \) \(\frac{{SE}}{{SI}} = \frac{{SA}}{{SF}}\)

 (c.g.c)

                                                        \( \Rightarrow \widehat {SIF} = \widehat {SEA}\)

\( \Rightarrow \) tứ giác AIFE nội tiếp (dấu hiệu nhận biết)

Mà 4 điểm A, E, H, F cũng cùng thuộc 1 đường tròn

\( \Rightarrow \) 5 điểm A, I, E, H, F cùng thuộc 1 đường tròn

\( \Rightarrow AIHE\) nội tiếp đường tròn

\( \Rightarrow \widehat {AIH} = \widehat {AEH} = {90^0} \Rightarrow IH \bot SA\)

 (c) Gọi M là trung điểm của BC, kẻ đường kính AD của (O). Chứng minh ba điểm H, M, D thẳng hàng và H là trực tâm tam giác ASM.

Xét (O): \(\widehat {ABD} = \widehat {ACD} = {90^0}\;\)(góc nội tiếp chắn nửa đường tròn)

\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{AB \bot BD}\\{AC \bot AD}\end{array}} \right.\)                mà  \(\left\{ {\begin{array}{*{20}{c}}{CH \bot AB}\\{BH \bot AC}\end{array}} \right.\)

\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{CH\parallel BD}\\{BH\parallel CD}\end{array}} \right.\)

\( \Rightarrow \) tứ giác BHCD là hình bình hành

\( \Rightarrow BC\) và \(HD\) cắt nhau.

d) Giả sử T là điểm nằm trên đoạn thẳng HC sao cho AT vuông gó(a+b)c với BT. Chứng minh hai đường tròn ngoại tiếp của tam giác IST và tam giác ECT tiếp xúc với nhau.