Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O), các đường cao BE và CF cắt nhau tại H. Gọi S là giao điểm của đường thẳng BC và EF; I là giao điểm của SA và đường tròn (O) (với I khác A).
a) Chứng minh rằng tứ giác AFHE là tứ giác nội tiếp.
b) Chứng minh \(SF.SE = SI.SA\) và \(HI \bot SA\).
c) Gọi M là trung điểm của BC, kẻ đường kính AD của (O). Chứng minh ba điểm H, M, D thẳng hàng và H là trực tâm tam giác ASM.
d) Giả sử T là điểm nằm trên đoạn thẳng HC sao cho AT vuông góc với BT. Chứng minh hai đường tròn ngoại tiếp của tam giác IST và tam giác ECT tiếp xúc với nhau.
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O), các đường cao BE và CF cắt nhau tại H. Gọi S là giao điểm của đường thẳng BC và EF; I là giao điểm của SA và đường tròn (O) (với I khác A).
a) Chứng minh rằng tứ giác AFHE là tứ giác nội tiếp.
b) Chứng minh \(SF.SE = SI.SA\) và \(HI \bot SA\).
c) Gọi M là trung điểm của BC, kẻ đường kính AD của (O). Chứng minh ba điểm H, M, D thẳng hàng và H là trực tâm tam giác ASM.
d) Giả sử T là điểm nằm trên đoạn thẳng HC sao cho AT vuông góc với BT. Chứng minh hai đường tròn ngoại tiếp của tam giác IST và tam giác ECT tiếp xúc với nhau.
Quảng cáo
Trả lời:
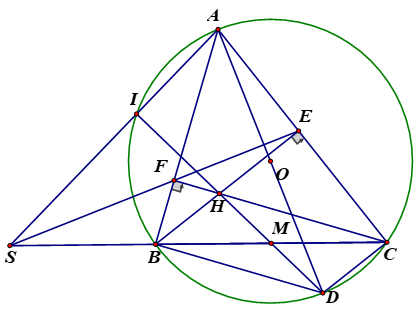
a) Chứng minh rằng tứ giác AFHE là tứ giác nội tiếp.
Do \(BE \bot AC;CF \bot AB \Rightarrow \widehat {AEB} = \widehat {AFC} = {90^0}\)
Xét tứ giác AEHF có: \(\widehat {AEH} + \widehat {AFH} = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow \) Tứ giác AEHF nội tiếp đường tròn.
b) Chứng minh \(SF.SE = SI.SA\) và \(HI \bot SA\).
Xét tứ giác BFEC có : \(\widehat {BFC} = \widehat {BEC} = {90^0}\)
Mà 2 góc này cùng nhìn cạnh BC
\( \Rightarrow \) Tứ giác BFEC nội tiếp đường tròn.
\( \Rightarrow \widehat {FEB} = \widehat {FCB}\) (hai góc nội tiếp cùng chắn cung BF)
Xét tam giác SEB và tam giác SCF có:
\(\widehat {ESC}\;\) là góc chung
\(\widehat {SEB} = \widehat {SCF}\)
(g-g)
\( \Rightarrow \frac{{SE}}{{SC}} = \frac{{SB}}{{SF}} \Rightarrow SE.SF = SB.SC\;\;\left( 1 \right)\)
Xét tam giác SAB và tam giác SCI có:
\(\widehat {ASC}\;\)chung
\(\widehat {SAB} = \widehat {SCI} = \frac{1}{2}\;\)số đo cung IB (góc nội tiếp)
(g-g)
\( \Rightarrow \frac{{SA}}{{SC}} = \frac{{SB}}{{SI}} \Rightarrow SA.SI = SB.SC\;\;\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow SE.SF = SA.SI\; \Rightarrow \) \(\frac{{SE}}{{SI}} = \frac{{SA}}{{SF}}\)
(c.g.c)
\( \Rightarrow \widehat {SIF} = \widehat {SEA}\)
\( \Rightarrow \) tứ giác AIFE nội tiếp (dấu hiệu nhận biết)
Mà 4 điểm A, E, H, F cũng cùng thuộc 1 đường tròn
\( \Rightarrow \) 5 điểm A, I, E, H, F cùng thuộc 1 đường tròn
\( \Rightarrow AIHE\) nội tiếp đường tròn
\( \Rightarrow \widehat {AIH} = \widehat {AEH} = {90^0} \Rightarrow IH \bot SA\)
(c) Gọi M là trung điểm của BC, kẻ đường kính AD của (O). Chứng minh ba điểm H, M, D thẳng hàng và H là trực tâm tam giác ASM.
Xét (O): \(\widehat {ABD} = \widehat {ACD} = {90^0}\;\)(góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{AB \bot BD}\\{AC \bot AD}\end{array}} \right.\) mà \(\left\{ {\begin{array}{*{20}{c}}{CH \bot AB}\\{BH \bot AC}\end{array}} \right.\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{CH\parallel BD}\\{BH\parallel CD}\end{array}} \right.\)
\( \Rightarrow \) tứ giác BHCD là hình bình hành
\( \Rightarrow BC\) và \(HD\) cắt nhau.
d) Giả sử T là điểm nằm trên đoạn thẳng HC sao cho AT vuông gó(a+b)c với BT. Chứng minh hai đường tròn ngoại tiếp của tam giác IST và tam giác ECT tiếp xúc với nhau.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
+ Phương trình có 2 nghiệm \({x_1},{x_2} \Leftrightarrow \Delta ' \ge 0 \Leftrightarrow {m^2} - \left( {{m^2} - m + 1} \right) \ge 0\)
\( \Leftrightarrow m - 1 \ge 0 \Leftrightarrow m \ge 1.\)
+ Theo hệ thức Vi-ét: \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2m\;\;\;\;\;\;\;\;}\\{{x_1}{x_2} = {m^2} - m + 1}\end{array}} \right.\)
+ Ta có: \(x_2^2 - x_1^2 + 4m{x_1} = 16 \Leftrightarrow x_2^2 - x_1^2 + 2\left( {{x_1} + {x_2}} \right).{x_1} = 16\)
\( \Leftrightarrow x_2^2 - x_1^2 + 2x_1^2 + 2{x_1}{x_2} = 16 \Leftrightarrow x_1^2 + x_2^2 + 2{x_1}{x_2} = 16\)
\( \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} = 16 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 4}\\{{x_1} + {x_2} = - 4}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2m = 4\;\;\;\;}\\{2m = - 4}\end{array}} \right.} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 2\;\;\left( {nhan} \right)}\\{m = - 2\;\;\left( {loai} \right)}\end{array}} \right.\)
Kết luận: Vậy \(m = 2\) thỏa mãn yêu cầu bài toán.
Lời giải
\(\frac{{1 + \sqrt {1 + {x^2}} }}{x} + \frac{{1 + \sqrt {1 + {y^2}} }}{y} + \frac{{1 + \sqrt {{z^2}} }}{z} \le xyz.\)
Từ \(x + y + z = zyz\; \Rightarrow \). \(\frac{1}{{xy}} + \frac{1}{{yz}} + \frac{1}{{xz}}\) = 1
Lại có: \(\frac{{\sqrt {1 + {x^2}} }}{x} = \sqrt {\frac{1}{{{x^2}}} + } = \sqrt {\frac{1}{{{x^2}}} + \frac{1}{{xy}} + \frac{1}{{yz}} + \frac{1}{{xz}}} \) (áp dụng \(\sqrt {ab} \le \frac{1}{2}\left( {a + b} \right)\))
\( \Rightarrow \frac{{1 + \sqrt {1 + {x^2}} }}{x} \le \frac{2}{x} + \frac{1}{{2y}} + \frac{1}{{2z}} \Rightarrow \frac{{1 + \sqrt {1 + {x^2}} }}{x} \le 3\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right)\)
Dấu “=” xảy ra \( \Leftrightarrow x = y = z\)
Chứng minh:
\(3\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right) \le xyz\)
\( \Leftrightarrow 3\left( {xy + yz + zx} \right) \le {\left( {xyz} \right)^2}\)
\( \Leftrightarrow 3\left( {xy + yz + zx} \right) \le {\left( {x + y + z} \right)^2}\)
\( \Leftrightarrow {\left( {x - y} \right)^2}2 + {\left( {y - z} \right)^2} + {\left( {z - x} \right)^2} \ge 0\) (đúng)
Vậy bất đẳng thức được chứng minh. Dấu “=” xảy ra khi \(x = y = z = \sqrt 3 .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.