PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một xe ô tô đang chạy với vận tốc \(65\) \({\rm{km/h}}\) thì người lái xe bất ngờ phát hiện chướng ngại vật trên đường cách đó \(50\;{\rm{m}}\). Người lái xe phản ứng một giây, sau đó đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ \[v\left( t \right) = - 10t + 20\;\left( {{\rm{m/s}}} \right)\], trong đó \(t\) là thời gian tính bằng giây kể từ lúc đạp phanh. Gọi \(s\left( t \right)\) là quãng đường xe ô tô đi được trong \(t\) (giây) kể từ lúc đạp phanh.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một xe ô tô đang chạy với vận tốc \(65\) \({\rm{km/h}}\) thì người lái xe bất ngờ phát hiện chướng ngại vật trên đường cách đó \(50\;{\rm{m}}\). Người lái xe phản ứng một giây, sau đó đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ \[v\left( t \right) = - 10t + 20\;\left( {{\rm{m/s}}} \right)\], trong đó \(t\) là thời gian tính bằng giây kể từ lúc đạp phanh. Gọi \(s\left( t \right)\) là quãng đường xe ô tô đi được trong \(t\) (giây) kể từ lúc đạp phanh.
Quảng cáo
Trả lời:
a) Đ, b) Đ, c) S, d) Đ
a) Do \(s'(t) = v(t)\) nên quãng đường \(s(t)\) mà xe ô tô đi được trong thời gian \(t\) (giây) là một nguyên hàm của hàm số \(v(t)\).
b) Ta có: \(\int {( - 10t + 20)} dt = - 5{t^2} + 20t + C\) với \(C\) là hằng số.
Khi đó, ta gọi hàm số \(s(t) = - 5{t^2} + 20t + C\).
Do \(s(0) = 0\) nên \(C = 0\). Suy ra \(s(t) = - 5{t^2} + 20t\).
c) Xe ô tô dừng hẳn khi \(v(t) = 0\) hay \( - 10t + 20 = 0 \Leftrightarrow t = 2\).
Vậy thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 2 giây.
d) Ta có xe ô tô đang chạy với tốc độ \(65\;{\rm{km/h}} \approx 18\;{\rm{m/s}}\).
Do đó, quãng đường xe ô tô còn di chuyển được kể từ lúc đạp phanh đến khi xe dừng hẳn là: \(s(2) = - 5 \cdot {2^2} + 20 \cdot 2 = 20\,{\rm{(m)}}\).
Vậy quãng đường xe ô tô đã di chuyển kể từ lúc người lái xe phát hiện chướng ngại vật trên đường đến khi xe ô tô dừng hẳn là: \(18 + 20 \approx 38\,{\rm{(m)}}\).
Do \(38 < 50\) nên xe ô tô đã dừng hẳn trước khi va chạm với chướng ngại vật trên đường.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: B
Ta có \(V = \pi \int\limits_0^\pi {{{\sin }^2}xdx} = \left. {\pi \left( {\frac{x}{2} - \frac{{\sin 2x}}{4}} \right)} \right|_0^\pi = \pi .\frac{\pi }{2} = \frac{{{\pi ^2}}}{2}\).
Lời giải
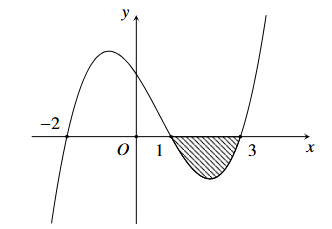
Trả lời: 1,3
Ta có \(\int\limits_{ - 2}^3 {f'\left( x \right)dx} = \int\limits_{ - 2}^1 {f'\left( x \right)dx} + \int\limits_1^3 {f'\left( x \right)dx} = 3 - \int\limits_1^3 {\left| {f'\left( x \right)} \right|dx} \)\( = 3 - \frac{5}{3} = \frac{4}{3}\).
Mà \(\int\limits_{ - 2}^3 {f'\left( x \right)dx} = \left. {f\left( x \right)} \right|_{ - 2}^3 = f\left( 3 \right) - f\left( { - 2} \right)\).
Do đó \(f\left( 3 \right) - f\left( { - 2} \right) \approx 1,3\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.