1) Tìm tất cả các cặp số nguyên dương (x;y) thỏa mãn
\({4^x} + \left( {1 + {3^y}} \right)\left( {1 + {7^y}} \right) = {2^x}\left( {{3^y} + {7^y} + 2} \right)\)
2) Với x,y,z là những số thực dương, tìm giá trị nhỏ nhất của biểu thức:
\(M = \frac{{{x^{14}} - {x^6} + 3}}{{{x^2}{y^2} + zx + zy}} + \frac{{{y^{14}} - {y^6} + 3}}{{{y^2}{z^2} + xy + xz}} + \frac{{{z^{14}} - {z^6} + 3}}{{{z^2}{x^2} + yz + yx}}\)
1) Tìm tất cả các cặp số nguyên dương (x;y) thỏa mãn
\({4^x} + \left( {1 + {3^y}} \right)\left( {1 + {7^y}} \right) = {2^x}\left( {{3^y} + {7^y} + 2} \right)\)
2) Với x,y,z là những số thực dương, tìm giá trị nhỏ nhất của biểu thức:
\(M = \frac{{{x^{14}} - {x^6} + 3}}{{{x^2}{y^2} + zx + zy}} + \frac{{{y^{14}} - {y^6} + 3}}{{{y^2}{z^2} + xy + xz}} + \frac{{{z^{14}} - {z^6} + 3}}{{{z^2}{x^2} + yz + yx}}\)
Quảng cáo
Trả lời:
1) Cách 1. Ta có các biến đổi phương trình sau
\({4^x} + \left( {1 + {3^y}} \right)\left( {1 + {7^y}} \right) = {2^x}\left( {{3^y} + {7^y} + 2} \right)\)
\( \Leftrightarrow {2^{2x}} - 1 + 2 + {3^y} + {7^y} + {21^y} = {2^x}\left( {{3^y} + {7^y} + 2} \right)\)
\( \Leftrightarrow \left( {{2^x} - 1} \right)\left( {{3^y} + {7^y} + 1 - {2^k}} \right) = {21^y}\) (1)
Ta chứng minh UCLN \(\left( {{2^x} - 1;{3^x} + {7^y} + 1 - {2^x}} \right) = 1\;\).Thật vậy, nếu UCLN(\({2^x} - 1;{3^x} + {7^y} + 1 - {2^x}\) ) > 1 thì gọi p là ước nguyên tố chung của \({2^x} - 1,{3^x} + {7^y} + 1 - {2^x}\). Suy ra p |\({3^y} + {7^y}\) . chú ý là \({3^y} + {7^y}\;\)đều không chia hết cho 3, 7 nên \(p \ne 3,7.\) Lại có p|\({21^y}\) nên p \( \in \){3, 7} mâu thuẫn.
Vậy UCLN\(\left( {{2^x} - 1;{3^x} + {7^y} + 1 - {2^x}} \right) = 1\;\) Ta xét hai trường hợp sau
· Nếu x là số chẵn thì \({2^x} - 1\) chia hết cho 3 và \({3^x} + {7^y} + 1 - {2^x}\;\)chia 3 dư 1.
Khi đó, từ phương trình (1) ta có
\(\left\{ {\begin{array}{*{20}{c}}{{2^x} - 1 = {3^y}}\\{{3^x} + {7^y} + 1 - {2^x} = {7^y}}\end{array}} \right.\)
Suy ra \({2^x} = {3^y} + 1\) ,Chi ý là \({3^y} \equiv 1,3\) (mod 8) nên \({3^y} + 1\) không chia hết cho 8. Từ đó \(x = 2\;v\`a \;y = 1\). . Vậy (x, y) = (2, 1)
· Nếu x là số lẻ thì \({2^x} - 1\) chia 3 dư 1 và \({3^x} + {7^y} + 1 - {2^x}\;\)chia hết cho 3.
Khi đó, từ phương trình (1) ta có
\(\left\{ {\begin{array}{*{20}{c}}{{2^x} - 1 = {7^y}}\\{{3^x} + {7^y} + 1 - {2^x} = {3^y}}\end{array}} \right.\)
Suy ra \({2^x} = {7^y} + 1\). Về phải chia 7 dư 1 nên về trái chia 7 dư 1. Từ đó \(x = 3k,k \in N\)* và thay vào phương trình được
\(\left( {{2^k} - 1} \right)\left( {{2^{2k}} + {2^k} + 1} \right) = {7^y}\)
Vì UCLN \(\left( {{2^k} - 1;{2^{2k}} + {2^k} + 1} \right) \in \left\{ {1,3} \right\}\) nên UCLN\(\left( {{2^k} - 1;{2^{2k}} + {2^k} + 1} \right) = 1.\;\)Vì \({2^{2k}} + {2^k} + 1 > 1\;\)nên \({2^k} - 1 = 1\) suy ra \(k = 1\)và \({7^y} = 7\) nên \(y = 1\) và \(x = 3k = 3\). Vậy \(\left( {x,y} \right) = \left( {3,1} \right).\)
Vậy tất cả các cặp số (x, y) thỏa mãn là (2, 1), (3, 1) .
Cách 2. Phương trình đã cho có thể viết lại thành
\(\left( {{2^x} - {7^y} - 1} \right)\left( {{2^x} - {3^y} - 1} \right) = 0\)
Tới đây giải giống hai trường hợp ở trên.
2) Ta có \(3\left( {{x^{14}} - {x^6} + 3} \right) = \left( {3{x^{14}} + 4} \right) - 3{x^6} + 5 \ge 7{x^6} - 3{x^6} + 5 = 4{x^6} + 5\)
theo bất đẳng thức AM-GM. Lại có cũng theo bất đẳng thức AM-GM, thì
\(4{x^6} + 5 = \left( {{x^6} + {x^6} + 1} \right) + \left( {{x^6} + {x^6} + 1} \right) + 3 \ge 3\left( {{x^4} + {x^4} + 1} \right) \ge 3\left( {{x^4} + 2{x^2}} \right)\)
Suy ra
\(M \ge \sum \frac{{{x^4}}}{{{x^2}{y^2} + xz + yz}} + 2\sum \frac{{{x^2}}}{{{x^2}{y^2} + xz + yz}}\)
và áp dụng bất đẳng thức cộng mẫu cho về trái, ta có
\(M \ge \frac{{{{\left( {{x^2} + {y^2} + {z^2}} \right)}^2} + 2{{(x + y + z)}^2}}}{{{x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2} + 2\left( {xy + yz + zx} \right)}} \ge \frac{{3\left( {{x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2}} \right) + 6\left( {xy + yz + zx} \right)}}{{{x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2} + 2\left( {xy + yz + zx} \right)}} = 3\)
Dấu bằng xảy ra khi và chỉ khi x = y = z = 1 Giá trị nhỏ nhất của M là 3.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
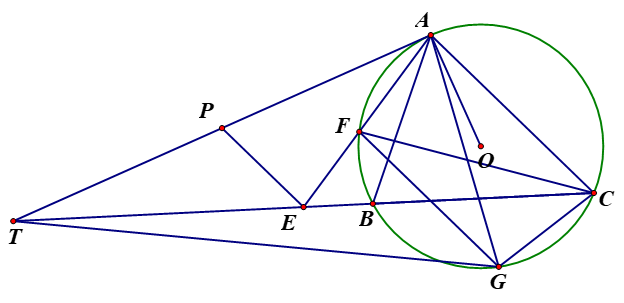
1) Vì AT là tiếp tuyến của nên ta được \(T{A^2} = TB.TC\). Như vậy, ta được
\(TP.TA = \frac{1}{2}T{A^2} = \frac{1}{2}TB.TC = TB.TE\) và vì tứ giác APEB là tứ giác nội tiếp.
2) Vì EP là đường trung bình của \(\Delta \) TAC , \(\Delta \) FGC là hình thang cân và AT là tiếp tuyến của (O) nên ta thu được \(\widehat {AEP} = \widehat {EAC} = \widehat {FAC} = \widehat {GCA} = \widehat {TAG}\)và \(\widehat {GAC} = \widehat {FCA} = \widehat {TAF} = \widehat {PAE}.\;\)Như vậy, ta được \(\Delta \) AEP \(\~\;\Delta \)ACG (g-g) và dẫn đến \(\frac{{AE}}{{AC}} = \frac{{AP}}{{AG}}\;\) . Lại chú ý \(AT = 2AP\) và \(AC = 2EP\), ta thu được \(\frac{{AE}}{{EP}} = \frac{{2AE}}{{AC}} = \frac{{2AP}}{{AG}} = \frac{{AT}}{{AG}}\). Kết hợp với \(\widehat {AEP} = \widehat {TAG}\) ta thu được \(\Delta \;AEP\;\~\;\Delta \;TAG\) (C.G.C) và vì thế \(\widehat {ATG} = \widehat {TAF}.\)
3) ta xét bổ đề sau:
∆ABC, đường thẳng qua B vuông AC cắt AC,(ABC) tại F,D. E thuộc (ABC) thoả DE//AC. Đường thẳng qua E vuông EF cắt BF tại G, đg thẳng qua B vuông AG cắt đường thẳng qua C vuông AD tại H, L trung điểm AH. CMR AEL = 90
Giải: BH giao EG tại J khi đó J thuộc (BFE). Mặt khác gọi K trung điểm BC thì F,K,J thẳng do BFK = ABE = BEJ = BFJ. Mà do FK vuông AD vuông CH nên J là trung điểm BH => JL // AB nên L thuộc EG => đpcm
Quay lại bài toán: Dựng hbh DKNG, DS' là đg kính của (ADG) khi đó KS'D = AS'D = AGD = DNK => S trùng S'. NG giao BC tại F, NE vuông AD tại E. Khi đó A,F,E,G cùng thuộc 1 đg tròn ( EF = DN = AG )
• Đường thẳng qua E vuông AF cắt đg thẳng qua T vuông AS tại J. Khi đó theo bổ đề, trung điểm Q' của AJ thuộc SG ( để ý T thuộc (AFGE) ). Mà Q'P vuông AS => Q' trùng Q. Hơn nữa biến đổi tỉ số cho ta R là trung điểm AE nên QR // JE vuông AF kết hợp thêm nếu cho JE cắt AF tại A' thì A' thuộc (EF) hay A' thuộc (DN) nên ta có đpcm.
Lời giải
1) Điều kiện: \(0 \le x < 5\;\) . Ta biến đổi phương trình thành
\(x + 2\sqrt x \sqrt {4x + 6} + 4x + 6 = 4x + 4\sqrt x \sqrt {5 - x} + 5 - x\)
Sử dụng hằng đẳng thức, ta thu được
\({(\sqrt x + \sqrt {4x + 6} )^2} = {(2\sqrt x + \sqrt {5 - x} )^2}\)
Suy ra \(\sqrt x + \sqrt {4x + 6} = 2\sqrt x + \sqrt {5 - x} \) (do từng vế đều không âm), hay
\(\sqrt {4x + 6} = \sqrt x + \sqrt {5 - x} \)
Bình phương hai vế của phương trình này ta có
\(4x + 6 = x + 5 - x + 2\sqrt {x\left( {5 - x} \right)} \)
Hay \(4x + 1 = 2\sqrt {x\left( {5 - x} \right)} \). Tiếp tục hay Tiếp tục ta bình phương hai vế với điều kiện \(4x + 1 \ge 0\;\) (đã thoả mãn được )
\(16{x^2} + 8x + 1 = 4x\left( {5 - x} \right)\)
Giải phương trình trên ta thu được \(x = \frac{1}{2}\;v\`a \;x = \frac{1}{{10}}\;\) (đều thoả mãn điều kiện).
Vậy, phương trình đã cho có đúng hai nghiệm \(x = \frac{1}{2}\;,\;x = \frac{1}{{10}}\;\)
2) Đặt \(S = x + y,\;P = xy\) . Ta có
\({x^3} + {y^3} = {(x + y)^3} - 3xy\left( {x + y} \right) = {S^3} - 3SP\)
Khi đó hệ phương trình trở thành
\(\left\{ {\begin{array}{*{20}{c}}{SP = 30}\\{{S^3} - 3SP = 30 + \sqrt[3]{{S + 120}}}\end{array}} \right.\)
Thay SP = 30 vào phương trình thứ hai ta có
\({S^3} = 120 + \sqrt[3]{{S + 120}}\)
hay \({S^3} + S = \left( {S + 120} \right) + \sqrt[3]{{S + 120}}\) Ta nhận thấy
Nếu \(S > \sqrt[3]{{S + 120}}\) thì\(\;{S^3} > S + 120\) , suy ra
\({S^3} + S > \left( {S + 120} \right) + \sqrt[3]{{S + 120}}\)
loại.
Nếu \(S < \sqrt[3]{{S + 120}}\) thì\(\;{S^3} < S + 120\) suy ra
\({S^3} + S < \left( {S + 120} \right) + \sqrt[3]{{S + 120}}\)
loại.
Như vậy ta có \(S = \sqrt[3]{{S + 120}},\;hay\;{S^3} - S - 120{\rm{\;}}\;\) Giải phương trình ta thu được S = 5 khi đó \(P = \;\frac{{30}}{S} = 6\). Vậy ta có
\(\left\{ {\begin{array}{*{20}{c}}{x + y = 5}\\{xy = 6}\end{array}} \right.\)
Theo Vi-ét đảo thì x,y là hai nghiệm của phương trình
\({x^2} - 5x + 6 = 0\)
Giải phương trình ta được \(\left( {x,y} \right) = \left( {2,3} \right),\left( {3,2} \right).\)
Vậy hệ đã cho có hai nghiệm (x,y) là \(\left( {2,3} \right)\) và \(\left( {3,2} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.