Cho tam giác ABC nhọn với AB < AC nội tiếp trong đường tròn (O) có tiếp tuyến tại A của (O) cắt BC ở T sao cho TB > BC Gọi P và E lần lượt là trung điểm của TA và TC.
1) Chứng minh rằng tứ giác APEB nội tiếp.
2) Gọi giao điểm thứ hai của AE với (O) là F. Láy G thuộc (O) sao cho FG song song với AC. Chửng minh rằng \(\widehat {ATG} = \widehat {TAF}.\)
3) Gọi H là trực tâm của tam giác ABC,D là giao điểm của AH và BC. M là trung điểm BC. K đối xứng với A qua BC. N thuộc đường thẳng AM sao cho KN song song với HM. Lấy S thuộc BC sao cho NS \( \bot \) NK . Dựng R thuộc tia AK sao cho AR.AH = \(A{D^2}.\;\)Q là điểm sao cho PQ \( \bot \) AS và SQ \( \bot \) AO . Chứng minh rằng điểm đối xứng của A qua QR thuộc đường tròn đường kinh DN.
Cho tam giác ABC nhọn với AB < AC nội tiếp trong đường tròn (O) có tiếp tuyến tại A của (O) cắt BC ở T sao cho TB > BC Gọi P và E lần lượt là trung điểm của TA và TC.
1) Chứng minh rằng tứ giác APEB nội tiếp.
2) Gọi giao điểm thứ hai của AE với (O) là F. Láy G thuộc (O) sao cho FG song song với AC. Chửng minh rằng \(\widehat {ATG} = \widehat {TAF}.\)
3) Gọi H là trực tâm của tam giác ABC,D là giao điểm của AH và BC. M là trung điểm BC. K đối xứng với A qua BC. N thuộc đường thẳng AM sao cho KN song song với HM. Lấy S thuộc BC sao cho NS \( \bot \) NK . Dựng R thuộc tia AK sao cho AR.AH = \(A{D^2}.\;\)Q là điểm sao cho PQ \( \bot \) AS và SQ \( \bot \) AO . Chứng minh rằng điểm đối xứng của A qua QR thuộc đường tròn đường kinh DN.
Quảng cáo
Trả lời:
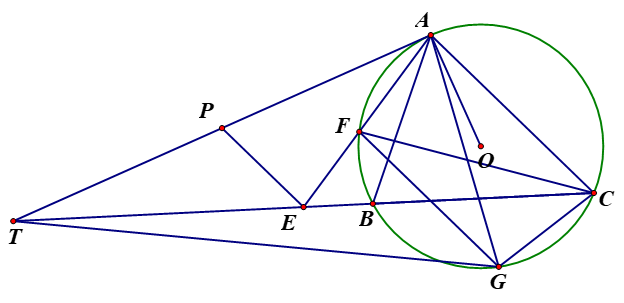
1) Vì AT là tiếp tuyến của nên ta được \(T{A^2} = TB.TC\). Như vậy, ta được
\(TP.TA = \frac{1}{2}T{A^2} = \frac{1}{2}TB.TC = TB.TE\) và vì tứ giác APEB là tứ giác nội tiếp.
2) Vì EP là đường trung bình của \(\Delta \) TAC , \(\Delta \) FGC là hình thang cân và AT là tiếp tuyến của (O) nên ta thu được \(\widehat {AEP} = \widehat {EAC} = \widehat {FAC} = \widehat {GCA} = \widehat {TAG}\)và \(\widehat {GAC} = \widehat {FCA} = \widehat {TAF} = \widehat {PAE}.\;\)Như vậy, ta được \(\Delta \) AEP \(\~\;\Delta \)ACG (g-g) và dẫn đến \(\frac{{AE}}{{AC}} = \frac{{AP}}{{AG}}\;\) . Lại chú ý \(AT = 2AP\) và \(AC = 2EP\), ta thu được \(\frac{{AE}}{{EP}} = \frac{{2AE}}{{AC}} = \frac{{2AP}}{{AG}} = \frac{{AT}}{{AG}}\). Kết hợp với \(\widehat {AEP} = \widehat {TAG}\) ta thu được \(\Delta \;AEP\;\~\;\Delta \;TAG\) (C.G.C) và vì thế \(\widehat {ATG} = \widehat {TAF}.\)
3) ta xét bổ đề sau:
∆ABC, đường thẳng qua B vuông AC cắt AC,(ABC) tại F,D. E thuộc (ABC) thoả DE//AC. Đường thẳng qua E vuông EF cắt BF tại G, đg thẳng qua B vuông AG cắt đường thẳng qua C vuông AD tại H, L trung điểm AH. CMR AEL = 90
Giải: BH giao EG tại J khi đó J thuộc (BFE). Mặt khác gọi K trung điểm BC thì F,K,J thẳng do BFK = ABE = BEJ = BFJ. Mà do FK vuông AD vuông CH nên J là trung điểm BH => JL // AB nên L thuộc EG => đpcm
Quay lại bài toán: Dựng hbh DKNG, DS' là đg kính của (ADG) khi đó KS'D = AS'D = AGD = DNK => S trùng S'. NG giao BC tại F, NE vuông AD tại E. Khi đó A,F,E,G cùng thuộc 1 đg tròn ( EF = DN = AG )
• Đường thẳng qua E vuông AF cắt đg thẳng qua T vuông AS tại J. Khi đó theo bổ đề, trung điểm Q' của AJ thuộc SG ( để ý T thuộc (AFGE) ). Mà Q'P vuông AS => Q' trùng Q. Hơn nữa biến đổi tỉ số cho ta R là trung điểm AE nên QR // JE vuông AF kết hợp thêm nếu cho JE cắt AF tại A' thì A' thuộc (EF) hay A' thuộc (DN) nên ta có đpcm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1) Cách 1. Ta có các biến đổi phương trình sau
\({4^x} + \left( {1 + {3^y}} \right)\left( {1 + {7^y}} \right) = {2^x}\left( {{3^y} + {7^y} + 2} \right)\)
\( \Leftrightarrow {2^{2x}} - 1 + 2 + {3^y} + {7^y} + {21^y} = {2^x}\left( {{3^y} + {7^y} + 2} \right)\)
\( \Leftrightarrow \left( {{2^x} - 1} \right)\left( {{3^y} + {7^y} + 1 - {2^k}} \right) = {21^y}\) (1)
Ta chứng minh UCLN \(\left( {{2^x} - 1;{3^x} + {7^y} + 1 - {2^x}} \right) = 1\;\).Thật vậy, nếu UCLN(\({2^x} - 1;{3^x} + {7^y} + 1 - {2^x}\) ) > 1 thì gọi p là ước nguyên tố chung của \({2^x} - 1,{3^x} + {7^y} + 1 - {2^x}\). Suy ra p |\({3^y} + {7^y}\) . chú ý là \({3^y} + {7^y}\;\)đều không chia hết cho 3, 7 nên \(p \ne 3,7.\) Lại có p|\({21^y}\) nên p \( \in \){3, 7} mâu thuẫn.
Vậy UCLN\(\left( {{2^x} - 1;{3^x} + {7^y} + 1 - {2^x}} \right) = 1\;\) Ta xét hai trường hợp sau
· Nếu x là số chẵn thì \({2^x} - 1\) chia hết cho 3 và \({3^x} + {7^y} + 1 - {2^x}\;\)chia 3 dư 1.
Khi đó, từ phương trình (1) ta có
\(\left\{ {\begin{array}{*{20}{c}}{{2^x} - 1 = {3^y}}\\{{3^x} + {7^y} + 1 - {2^x} = {7^y}}\end{array}} \right.\)
Suy ra \({2^x} = {3^y} + 1\) ,Chi ý là \({3^y} \equiv 1,3\) (mod 8) nên \({3^y} + 1\) không chia hết cho 8. Từ đó \(x = 2\;v\`a \;y = 1\). . Vậy (x, y) = (2, 1)
· Nếu x là số lẻ thì \({2^x} - 1\) chia 3 dư 1 và \({3^x} + {7^y} + 1 - {2^x}\;\)chia hết cho 3.
Khi đó, từ phương trình (1) ta có
\(\left\{ {\begin{array}{*{20}{c}}{{2^x} - 1 = {7^y}}\\{{3^x} + {7^y} + 1 - {2^x} = {3^y}}\end{array}} \right.\)
Suy ra \({2^x} = {7^y} + 1\). Về phải chia 7 dư 1 nên về trái chia 7 dư 1. Từ đó \(x = 3k,k \in N\)* và thay vào phương trình được
\(\left( {{2^k} - 1} \right)\left( {{2^{2k}} + {2^k} + 1} \right) = {7^y}\)
Vì UCLN \(\left( {{2^k} - 1;{2^{2k}} + {2^k} + 1} \right) \in \left\{ {1,3} \right\}\) nên UCLN\(\left( {{2^k} - 1;{2^{2k}} + {2^k} + 1} \right) = 1.\;\)Vì \({2^{2k}} + {2^k} + 1 > 1\;\)nên \({2^k} - 1 = 1\) suy ra \(k = 1\)và \({7^y} = 7\) nên \(y = 1\) và \(x = 3k = 3\). Vậy \(\left( {x,y} \right) = \left( {3,1} \right).\)
Vậy tất cả các cặp số (x, y) thỏa mãn là (2, 1), (3, 1) .
Cách 2. Phương trình đã cho có thể viết lại thành
\(\left( {{2^x} - {7^y} - 1} \right)\left( {{2^x} - {3^y} - 1} \right) = 0\)
Tới đây giải giống hai trường hợp ở trên.
2) Ta có \(3\left( {{x^{14}} - {x^6} + 3} \right) = \left( {3{x^{14}} + 4} \right) - 3{x^6} + 5 \ge 7{x^6} - 3{x^6} + 5 = 4{x^6} + 5\)
theo bất đẳng thức AM-GM. Lại có cũng theo bất đẳng thức AM-GM, thì
\(4{x^6} + 5 = \left( {{x^6} + {x^6} + 1} \right) + \left( {{x^6} + {x^6} + 1} \right) + 3 \ge 3\left( {{x^4} + {x^4} + 1} \right) \ge 3\left( {{x^4} + 2{x^2}} \right)\)
Suy ra
\(M \ge \sum \frac{{{x^4}}}{{{x^2}{y^2} + xz + yz}} + 2\sum \frac{{{x^2}}}{{{x^2}{y^2} + xz + yz}}\)
và áp dụng bất đẳng thức cộng mẫu cho về trái, ta có
\(M \ge \frac{{{{\left( {{x^2} + {y^2} + {z^2}} \right)}^2} + 2{{(x + y + z)}^2}}}{{{x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2} + 2\left( {xy + yz + zx} \right)}} \ge \frac{{3\left( {{x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2}} \right) + 6\left( {xy + yz + zx} \right)}}{{{x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2} + 2\left( {xy + yz + zx} \right)}} = 3\)
Dấu bằng xảy ra khi và chỉ khi x = y = z = 1 Giá trị nhỏ nhất của M là 3.
Lời giải
1) Điều kiện: \(0 \le x < 5\;\) . Ta biến đổi phương trình thành
\(x + 2\sqrt x \sqrt {4x + 6} + 4x + 6 = 4x + 4\sqrt x \sqrt {5 - x} + 5 - x\)
Sử dụng hằng đẳng thức, ta thu được
\({(\sqrt x + \sqrt {4x + 6} )^2} = {(2\sqrt x + \sqrt {5 - x} )^2}\)
Suy ra \(\sqrt x + \sqrt {4x + 6} = 2\sqrt x + \sqrt {5 - x} \) (do từng vế đều không âm), hay
\(\sqrt {4x + 6} = \sqrt x + \sqrt {5 - x} \)
Bình phương hai vế của phương trình này ta có
\(4x + 6 = x + 5 - x + 2\sqrt {x\left( {5 - x} \right)} \)
Hay \(4x + 1 = 2\sqrt {x\left( {5 - x} \right)} \). Tiếp tục hay Tiếp tục ta bình phương hai vế với điều kiện \(4x + 1 \ge 0\;\) (đã thoả mãn được )
\(16{x^2} + 8x + 1 = 4x\left( {5 - x} \right)\)
Giải phương trình trên ta thu được \(x = \frac{1}{2}\;v\`a \;x = \frac{1}{{10}}\;\) (đều thoả mãn điều kiện).
Vậy, phương trình đã cho có đúng hai nghiệm \(x = \frac{1}{2}\;,\;x = \frac{1}{{10}}\;\)
2) Đặt \(S = x + y,\;P = xy\) . Ta có
\({x^3} + {y^3} = {(x + y)^3} - 3xy\left( {x + y} \right) = {S^3} - 3SP\)
Khi đó hệ phương trình trở thành
\(\left\{ {\begin{array}{*{20}{c}}{SP = 30}\\{{S^3} - 3SP = 30 + \sqrt[3]{{S + 120}}}\end{array}} \right.\)
Thay SP = 30 vào phương trình thứ hai ta có
\({S^3} = 120 + \sqrt[3]{{S + 120}}\)
hay \({S^3} + S = \left( {S + 120} \right) + \sqrt[3]{{S + 120}}\) Ta nhận thấy
Nếu \(S > \sqrt[3]{{S + 120}}\) thì\(\;{S^3} > S + 120\) , suy ra
\({S^3} + S > \left( {S + 120} \right) + \sqrt[3]{{S + 120}}\)
loại.
Nếu \(S < \sqrt[3]{{S + 120}}\) thì\(\;{S^3} < S + 120\) suy ra
\({S^3} + S < \left( {S + 120} \right) + \sqrt[3]{{S + 120}}\)
loại.
Như vậy ta có \(S = \sqrt[3]{{S + 120}},\;hay\;{S^3} - S - 120{\rm{\;}}\;\) Giải phương trình ta thu được S = 5 khi đó \(P = \;\frac{{30}}{S} = 6\). Vậy ta có
\(\left\{ {\begin{array}{*{20}{c}}{x + y = 5}\\{xy = 6}\end{array}} \right.\)
Theo Vi-ét đảo thì x,y là hai nghiệm của phương trình
\({x^2} - 5x + 6 = 0\)
Giải phương trình ta được \(\left( {x,y} \right) = \left( {2,3} \right),\left( {3,2} \right).\)
Vậy hệ đã cho có hai nghiệm (x,y) là \(\left( {2,3} \right)\) và \(\left( {3,2} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.