Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Chuyên Khoa Học Tự Nhiên có đáp án
44 người thi tuần này 4.6 86 lượt thi 4 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
1) Điều kiện: \(0 \le x < 5\;\) . Ta biến đổi phương trình thành
\(x + 2\sqrt x \sqrt {4x + 6} + 4x + 6 = 4x + 4\sqrt x \sqrt {5 - x} + 5 - x\)
Sử dụng hằng đẳng thức, ta thu được
\({(\sqrt x + \sqrt {4x + 6} )^2} = {(2\sqrt x + \sqrt {5 - x} )^2}\)
Suy ra \(\sqrt x + \sqrt {4x + 6} = 2\sqrt x + \sqrt {5 - x} \) (do từng vế đều không âm), hay
\(\sqrt {4x + 6} = \sqrt x + \sqrt {5 - x} \)
Bình phương hai vế của phương trình này ta có
\(4x + 6 = x + 5 - x + 2\sqrt {x\left( {5 - x} \right)} \)
Hay \(4x + 1 = 2\sqrt {x\left( {5 - x} \right)} \). Tiếp tục hay Tiếp tục ta bình phương hai vế với điều kiện \(4x + 1 \ge 0\;\) (đã thoả mãn được )
\(16{x^2} + 8x + 1 = 4x\left( {5 - x} \right)\)
Giải phương trình trên ta thu được \(x = \frac{1}{2}\;v\`a \;x = \frac{1}{{10}}\;\) (đều thoả mãn điều kiện).
Vậy, phương trình đã cho có đúng hai nghiệm \(x = \frac{1}{2}\;,\;x = \frac{1}{{10}}\;\)
2) Đặt \(S = x + y,\;P = xy\) . Ta có
\({x^3} + {y^3} = {(x + y)^3} - 3xy\left( {x + y} \right) = {S^3} - 3SP\)
Khi đó hệ phương trình trở thành
\(\left\{ {\begin{array}{*{20}{c}}{SP = 30}\\{{S^3} - 3SP = 30 + \sqrt[3]{{S + 120}}}\end{array}} \right.\)
Thay SP = 30 vào phương trình thứ hai ta có
\({S^3} = 120 + \sqrt[3]{{S + 120}}\)
hay \({S^3} + S = \left( {S + 120} \right) + \sqrt[3]{{S + 120}}\) Ta nhận thấy
Nếu \(S > \sqrt[3]{{S + 120}}\) thì\(\;{S^3} > S + 120\) , suy ra
\({S^3} + S > \left( {S + 120} \right) + \sqrt[3]{{S + 120}}\)
loại.
Nếu \(S < \sqrt[3]{{S + 120}}\) thì\(\;{S^3} < S + 120\) suy ra
\({S^3} + S < \left( {S + 120} \right) + \sqrt[3]{{S + 120}}\)
loại.
Như vậy ta có \(S = \sqrt[3]{{S + 120}},\;hay\;{S^3} - S - 120{\rm{\;}}\;\) Giải phương trình ta thu được S = 5 khi đó \(P = \;\frac{{30}}{S} = 6\). Vậy ta có
\(\left\{ {\begin{array}{*{20}{c}}{x + y = 5}\\{xy = 6}\end{array}} \right.\)
Theo Vi-ét đảo thì x,y là hai nghiệm của phương trình
\({x^2} - 5x + 6 = 0\)
Giải phương trình ta được \(\left( {x,y} \right) = \left( {2,3} \right),\left( {3,2} \right).\)
Vậy hệ đã cho có hai nghiệm (x,y) là \(\left( {2,3} \right)\) và \(\left( {3,2} \right)\)
Lời giải
1) Cách 1. Ta có các biến đổi phương trình sau
\({4^x} + \left( {1 + {3^y}} \right)\left( {1 + {7^y}} \right) = {2^x}\left( {{3^y} + {7^y} + 2} \right)\)
\( \Leftrightarrow {2^{2x}} - 1 + 2 + {3^y} + {7^y} + {21^y} = {2^x}\left( {{3^y} + {7^y} + 2} \right)\)
\( \Leftrightarrow \left( {{2^x} - 1} \right)\left( {{3^y} + {7^y} + 1 - {2^k}} \right) = {21^y}\) (1)
Ta chứng minh UCLN \(\left( {{2^x} - 1;{3^x} + {7^y} + 1 - {2^x}} \right) = 1\;\).Thật vậy, nếu UCLN(\({2^x} - 1;{3^x} + {7^y} + 1 - {2^x}\) ) > 1 thì gọi p là ước nguyên tố chung của \({2^x} - 1,{3^x} + {7^y} + 1 - {2^x}\). Suy ra p |\({3^y} + {7^y}\) . chú ý là \({3^y} + {7^y}\;\)đều không chia hết cho 3, 7 nên \(p \ne 3,7.\) Lại có p|\({21^y}\) nên p \( \in \){3, 7} mâu thuẫn.
Vậy UCLN\(\left( {{2^x} - 1;{3^x} + {7^y} + 1 - {2^x}} \right) = 1\;\) Ta xét hai trường hợp sau
· Nếu x là số chẵn thì \({2^x} - 1\) chia hết cho 3 và \({3^x} + {7^y} + 1 - {2^x}\;\)chia 3 dư 1.
Khi đó, từ phương trình (1) ta có
\(\left\{ {\begin{array}{*{20}{c}}{{2^x} - 1 = {3^y}}\\{{3^x} + {7^y} + 1 - {2^x} = {7^y}}\end{array}} \right.\)
Suy ra \({2^x} = {3^y} + 1\) ,Chi ý là \({3^y} \equiv 1,3\) (mod 8) nên \({3^y} + 1\) không chia hết cho 8. Từ đó \(x = 2\;v\`a \;y = 1\). . Vậy (x, y) = (2, 1)
· Nếu x là số lẻ thì \({2^x} - 1\) chia 3 dư 1 và \({3^x} + {7^y} + 1 - {2^x}\;\)chia hết cho 3.
Khi đó, từ phương trình (1) ta có
\(\left\{ {\begin{array}{*{20}{c}}{{2^x} - 1 = {7^y}}\\{{3^x} + {7^y} + 1 - {2^x} = {3^y}}\end{array}} \right.\)
Suy ra \({2^x} = {7^y} + 1\). Về phải chia 7 dư 1 nên về trái chia 7 dư 1. Từ đó \(x = 3k,k \in N\)* và thay vào phương trình được
\(\left( {{2^k} - 1} \right)\left( {{2^{2k}} + {2^k} + 1} \right) = {7^y}\)
Vì UCLN \(\left( {{2^k} - 1;{2^{2k}} + {2^k} + 1} \right) \in \left\{ {1,3} \right\}\) nên UCLN\(\left( {{2^k} - 1;{2^{2k}} + {2^k} + 1} \right) = 1.\;\)Vì \({2^{2k}} + {2^k} + 1 > 1\;\)nên \({2^k} - 1 = 1\) suy ra \(k = 1\)và \({7^y} = 7\) nên \(y = 1\) và \(x = 3k = 3\). Vậy \(\left( {x,y} \right) = \left( {3,1} \right).\)
Vậy tất cả các cặp số (x, y) thỏa mãn là (2, 1), (3, 1) .
Cách 2. Phương trình đã cho có thể viết lại thành
\(\left( {{2^x} - {7^y} - 1} \right)\left( {{2^x} - {3^y} - 1} \right) = 0\)
Tới đây giải giống hai trường hợp ở trên.
2) Ta có \(3\left( {{x^{14}} - {x^6} + 3} \right) = \left( {3{x^{14}} + 4} \right) - 3{x^6} + 5 \ge 7{x^6} - 3{x^6} + 5 = 4{x^6} + 5\)
theo bất đẳng thức AM-GM. Lại có cũng theo bất đẳng thức AM-GM, thì
\(4{x^6} + 5 = \left( {{x^6} + {x^6} + 1} \right) + \left( {{x^6} + {x^6} + 1} \right) + 3 \ge 3\left( {{x^4} + {x^4} + 1} \right) \ge 3\left( {{x^4} + 2{x^2}} \right)\)
Suy ra
\(M \ge \sum \frac{{{x^4}}}{{{x^2}{y^2} + xz + yz}} + 2\sum \frac{{{x^2}}}{{{x^2}{y^2} + xz + yz}}\)
và áp dụng bất đẳng thức cộng mẫu cho về trái, ta có
\(M \ge \frac{{{{\left( {{x^2} + {y^2} + {z^2}} \right)}^2} + 2{{(x + y + z)}^2}}}{{{x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2} + 2\left( {xy + yz + zx} \right)}} \ge \frac{{3\left( {{x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2}} \right) + 6\left( {xy + yz + zx} \right)}}{{{x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2} + 2\left( {xy + yz + zx} \right)}} = 3\)
Dấu bằng xảy ra khi và chỉ khi x = y = z = 1 Giá trị nhỏ nhất của M là 3.
Lời giải
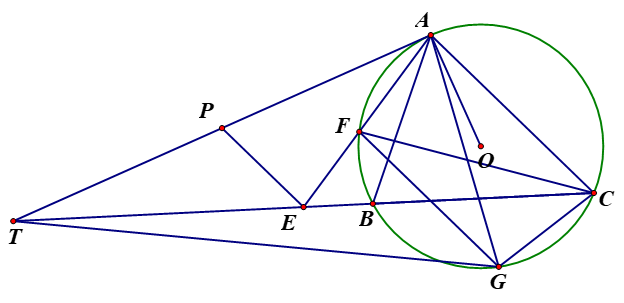
1) Vì AT là tiếp tuyến của nên ta được \(T{A^2} = TB.TC\). Như vậy, ta được
\(TP.TA = \frac{1}{2}T{A^2} = \frac{1}{2}TB.TC = TB.TE\) và vì tứ giác APEB là tứ giác nội tiếp.
2) Vì EP là đường trung bình của \(\Delta \) TAC , \(\Delta \) FGC là hình thang cân và AT là tiếp tuyến của (O) nên ta thu được \(\widehat {AEP} = \widehat {EAC} = \widehat {FAC} = \widehat {GCA} = \widehat {TAG}\)và \(\widehat {GAC} = \widehat {FCA} = \widehat {TAF} = \widehat {PAE}.\;\)Như vậy, ta được \(\Delta \) AEP \(\~\;\Delta \)ACG (g-g) và dẫn đến \(\frac{{AE}}{{AC}} = \frac{{AP}}{{AG}}\;\) . Lại chú ý \(AT = 2AP\) và \(AC = 2EP\), ta thu được \(\frac{{AE}}{{EP}} = \frac{{2AE}}{{AC}} = \frac{{2AP}}{{AG}} = \frac{{AT}}{{AG}}\). Kết hợp với \(\widehat {AEP} = \widehat {TAG}\) ta thu được \(\Delta \;AEP\;\~\;\Delta \;TAG\) (C.G.C) và vì thế \(\widehat {ATG} = \widehat {TAF}.\)
3) ta xét bổ đề sau:
∆ABC, đường thẳng qua B vuông AC cắt AC,(ABC) tại F,D. E thuộc (ABC) thoả DE//AC. Đường thẳng qua E vuông EF cắt BF tại G, đg thẳng qua B vuông AG cắt đường thẳng qua C vuông AD tại H, L trung điểm AH. CMR AEL = 90
Giải: BH giao EG tại J khi đó J thuộc (BFE). Mặt khác gọi K trung điểm BC thì F,K,J thẳng do BFK = ABE = BEJ = BFJ. Mà do FK vuông AD vuông CH nên J là trung điểm BH => JL // AB nên L thuộc EG => đpcm
Quay lại bài toán: Dựng hbh DKNG, DS' là đg kính của (ADG) khi đó KS'D = AS'D = AGD = DNK => S trùng S'. NG giao BC tại F, NE vuông AD tại E. Khi đó A,F,E,G cùng thuộc 1 đg tròn ( EF = DN = AG )
• Đường thẳng qua E vuông AF cắt đg thẳng qua T vuông AS tại J. Khi đó theo bổ đề, trung điểm Q' của AJ thuộc SG ( để ý T thuộc (AFGE) ). Mà Q'P vuông AS => Q' trùng Q. Hơn nữa biến đổi tỉ số cho ta R là trung điểm AE nên QR // JE vuông AF kết hợp thêm nếu cho JE cắt AF tại A' thì A' thuộc (EF) hay A' thuộc (DN) nên ta có đpcm.
Lời giải
Cách 1. Ta giải bài toán tổng quát: Điền các số 1.2.... \({n^{2\;}}\) với n > 1 vào các ô vuông của bảng cỡn nn Khi đó tồn tại hai ô vuông kề nhau (chung cạnh) chứa hai số x, y mà |x - y| \( \ge \) n Kí hiệu \({m_k},{M_k}\;\) tương ứng là số nhỏ nhất và số lớn nhất của hàng thứ k với k = 1, 2 ,...,n. Chú ý là \({m_1},{m_2},\) ...,\({m_n},{M_1},{M_2}, \ldots \ldots .,{M_n}\) đôi một phân biệt. Đặt
m= max (\({m_1},{m_2},\) ...,\({m_n}\) ) và M= min (\({M_1},{M_2}, \ldots \ldots .,{M_n}\) ) .
Xét hai trường hợp
· Nếu m < M thì ta có \({m_k} \le m \le {M_k}\;\) với mọi k = 1, 2 ,...,n. Điều này suy ra với hàng k bất kỷ thì tồn tại hai số \({a_k} \le m < {b_k}\;\) và với mỗi hàng k ta chọn cặp (\({a_k},{b_k}\;\) ) thuộc hai ô kề nhau ở hàng k. Vì \({b_1},{b_2}, \ldots ..{b_n}\) lớn hơn m và các số \({b_1},{b_2}, \ldots ..{b_n}\) là đôi một phân biệt nên tồn tại k \( \in \left\{ {1,2, \ldots .,n} \right\}\;\). sao cho \({b_k} \ge n + m\) và do đó
\({b_k} - {a_k} \ge \left( {m + n} \right) - m = n.\)
· Nếu m > M thì gọi i, j \( \in \{ \) 1, 2 ,...,n} là các chỉ số sao cho \({m_i}\) > M = \({M_j}\) Khi đó tại mỗi cột luôn tồn tại các số không vượt quá M (ví dụ như số hàng j) và các số lớn hơn M (ví dụ như số ở hàng i). Khi đó với cột k bất kỳ tồn tại \({a_k},{b_k}\;\) sao cho \({a_k} \le M < {b_k}\) và \({a_k},{b_k}\) thuộc hai ô kề nhau của cột k. Tương tự như trường hợp đầu tiên thì ta cũng có tồn tại k \( \in \{ \) 1, 2 ,...,n}mà \({b_k} \ge M + n\) . Suy ra
\({b_k} - {a_k} \ge \left( {M + n} \right) - m = n.\)
Trong mọi tình huống ta đều có điều phải chứng minh.
Cách 2. Giả sử phản chứng, tồn tại cách điền để không tồn tại x,y như vậy. Ta lần lượt điền các số bắt đầu từ 1 vào bảng ô vuông, xét thời điểm đầu tiên mà cả n cột đều đã được điền số. Ta xét hai trường hợp sau:
· Nếu tồn tại cột nào đó đã được phủ hoàn toàn, ta sẽ đổi vai trò của hàng và cột (xét thời điểm đầu tiên cả n hàng đều có số). Nếu khi đó lại tồn tại một hàng được phủ hoàn toàn, thì tức là hai thời điểm đang xét trùng nhau. Điều này là không thể vì ô vừa được thêm phải là ô cuối cùng của hàng và cột đó, xét thời điểm ngay trước đó cho ta tất cả các hàng đều đã được điền.
· Nếu không tồn tại cột đã phủ hoàn toàn, do mỗi cột đều có ô đã điền, ta có thể chọn ra ở cột thứ i được cặp ô \({A_i},{B_i}m\`a \;{A_i}\)được điền còn \({B_i}\;\)thì chưa.
Cần có \({B_i} - {A_i} \le n - 1\;\) kéo theo \({B_i} \le max\)(\({A_1},{A_2}, \ldots ..,{A_n}\)) + n -1,\(\forall i\)
Mà các số từ 1 đến max(\({A_i})\;\)đều đã được điền nên \({B_i} > {\rm{max}}\left( {{A_i}} \right)\), vô lý do n số \({B_i}\;\)phân biệt.
Các trường hợp cho ta giả sử sai và ta có điều phải chứng minh.