Rút gọn biểu thức \(A = \sqrt {{{\left( {\sqrt 2  - 1} \right)}^2}}  - \frac{1}{3}\sqrt {18} \).

1.Vẽ đồ thị hàm số \[y =  - 2{x^2}.\]

+ Hàm số xác định với mọi \(x \in \mathbb{R}\).

+ Bảng giá trị:

\(x\).–2.–1.0.1.2

\(y\).–8.–2.0.–2.–8

+ Nhận xét: Đồ thị hàm số \[y =  - 2{x^2}\] là một đường cong parabol đi qua gốc tọa độ \(O\left( {0;0} \right),\) nhận trục Oy làm trục đối xứng, nằm phía dưới trục hoành, điểm O là điểm cao nhất của đồ thị.

2.Tìm tham số thực m để đồ thị hàm số \[y =  - 2{x^2}\] và đường thẳng \[y = x - m\,\] có điểm chung.

Phương trình hoành độ giao điểm của đồ thị hàm số \[y =  - 2{x^2}\] và đường thẳng \[y = x - m\,\] là \( - 2{x^2} = x - m \Leftrightarrow 2{x^2} + x - m = 0\)                    

\(\Delta  = {1^2} - 4.2.\left( { - m} \right) = 1 + 8m.\)

Để đồ thị hàm số \[y =  - 2{x^2}\] và đường thẳng \[y = x - m\,\] có điểm chung thì \(\Delta  \ge 0 \Rightarrow 1 + 8m \ge 0 \Leftrightarrow m \ge  - \frac{1}{8} \cdot \)

Cách 1: Cho phương trình \[3{x^2} + 5x - 1 = 0\] có hai nghiệm \({x_1}\),\({x_2}\). Tính giá trị biểu thức \(T = 6{x_1} - 7{x_1}{x_2} + 6{x_2}\).

Vì \({x_1}\),\({x_2}\)là hai nghiệm của phương trình \[3{x^2} + 5x - 1 = 0\] nên

theo hệ thức Vi-ét thì \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \frac{b}{a} = \frac{{ - 5}}{3}\\{x_1}{x_2} = \frac{c}{a} = \frac{{ - 1}}{3}\end{array} \right.\).

\[T = 6{x_1} - 7{x_1}{x_2} + 6{x_2} = 6\left( {{x_1} + {x_2}} \right) - 7{x_1}{x_2}\]

  \[ = 6\left( {\frac{{ - 5}}{3}} \right) - 7.\left( {\frac{{ - 1}}{3}} \right) = \frac{{ - 23}}{3}\]

Cách 2: Cho phương trình \[3{x^2} + 5x - 1 = 0\] có hai nghiệm \({x_1}\),\({x_2}\). Tính giá trị biểu thức \(T = 6{x_1} - 7{x_1}{x_2} + 6{x_2}\).

3.Giải được hai nghiệm của phương trình \[3{x^2} + 5x - 1 = 0\]

\[{x_1} = \frac{{ - 5 + \sqrt {37} }}{6};{\rm{ }}{x_2} = \frac{{ - 5 - \sqrt {37} }}{6}\]

\[T = 6{x_1} - 7{x_1}{x_2} + 6{x_2} = 6 \cdot \frac{{ - 5 + \sqrt {37} }}{6} - 7 \cdot \frac{{ - 5 + \sqrt {37} }}{6} \cdot \frac{{ - 5 - \sqrt {37} }}{6} + 6 \cdot \frac{{ - 5 - \sqrt {37} }}{6}\]

   \[ = \frac{{ - 23}}{3}\]

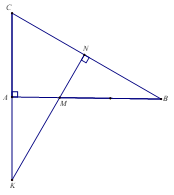
1.Chứng minh tứ giác AMNC nội tiếp.

Xét tứ giác AMNC có

\(\widehat {CAM} = \widehat {CAB} = {90^o}\)(\(\Delta ABC\) vuông tại A, \[M \in AB\]).

\(\widehat {CNM} = {90^o}\) (MN vuông góc BC).

Suy ra \(\widehat {CAM} + \widehat {CNM} = {90^o} + {90^0} = {180^0}\)

Vậy tứ giác AMNC nội tiếp (tổng hai góc đối bằng \({180^0}\)).

2.Chứng minh \(\widehat {ABK} = \widehat {ACM}.\)

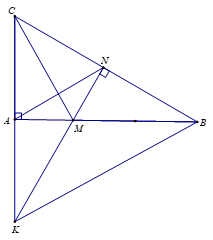
Xét tứ giác ANBK có

\(\widehat {KAB} = {90^o}\) (kề bù với góc vuông CAB).

\(\widehat {KNB} = \widehat {MNB} = {90^o}\) (MN vuông góc BC, K thuộc đường thẳng MN).

Suy ra \(\widehat {KAB} = \widehat {KNB} = {90^o}.\)

Vậy tứ giác ANBK nội tiếp (hai đỉnh A, N kề nhau cùng nhìn cạnh BK dưới một góc bằng \({90^0}\)).

\( \Rightarrow \widehat {ABK} = \widehat {ANK}\)(hai góc nội tiếp cùng chắn cung AK). (1)

Vì tứ giác AMNC nội tiếp (chứng minh câu 5.1)

nên \(\widehat {ANM} = \widehat {ACM}\)(hai góc nội tiếp cùng chắn cung AM).

hay \(\widehat {ANK} = \widehat {ACM}\)(K thuộc đường thẳng MN). (2)

Từ (1) và (2) suy ra \(\widehat {ABK} = \widehat {ACM}.\)

3.Chứng minh \(\frac{1}{r} = \frac{1}{{KN}} + \frac{1}{{CD}} + \frac{1}{{AB}} \cdot \)

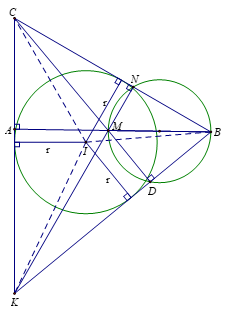
Xét \(\Delta BCK\)có BA là đường cao, KN là đường cao, M là giao điểm của BA và KN.

Suy ra M là trực tâm của \(\Delta BCK.\)

Do đó \(CM \bot BK.\) (1)

Xét đường tròn đường kính BM có \[\widehat {MDB} = {90^0}\] (góc nội tiếp chắn nửa đường tròn).

Suy ra \(MD \bot BK.\)(2)

Từ (1) và (2) suy ra ba điểm C, M, D thẳng hàng. Do đó \(CD \bot BK.\)

Diện tích \[\Delta BIC\]là \[{S_{BIC}} = \frac{1}{2}.r.BC\]

Diện tích \[\Delta BIK\]là \[{S_{BIK}} = \frac{1}{2}.r.BK\]

Diện tích \[\Delta CIK\]là \[{S_{CIK}} = \frac{1}{2}.r.CK\]

Diện tích \[\Delta BCK\]là \[{S_{BCK}} = \frac{1}{2}KN.BC = \frac{1}{2}BK.CD = \frac{1}{2}CK.AB\]

Suy ra \[\frac{1}{2}BC = \frac{{{S_{BCK}}}}{{KN}};{\rm{ }}\frac{1}{2}BK = \frac{{{S_{BCK}}}}{{CD}};{\rm{ }}\frac{1}{2}CK = \frac{{{S_{BCK}}}}{{AB}}\]

Mà \[{S_{BCK}} = {S_{BIC}} + {S_{BIK}} + {S_{CIK}}\]

hay \[{S_{BCK}} = r.\frac{{{S_{BCK}}}}{{KN}} + r.\frac{{{S_{BCK}}}}{{CD}} + r.\frac{{{S_{BCK}}}}{{AB}}\]

  \[ \Rightarrow {S_{BCK}} = r.{S_{BCK}}\left( {\frac{1}{{KN}} + \frac{1}{{CD}} + \frac{1}{{AB}}} \right)\]

Vậy \(\frac{1}{r} = \frac{1}{{KN}} + \frac{1}{{CD}} + \frac{1}{{AB}} \cdot \)