Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Đồng Nai có đáp án

1.Vẽ đồ thị hàm số \[y =  - 2{x^2}.\]

+ Hàm số xác định với mọi \(x \in \mathbb{R}\).

+ Bảng giá trị:

\(x\).–2.–1.0.1.2

\(y\).–8.–2.0.–2.–8

+ Nhận xét: Đồ thị hàm số \[y =  - 2{x^2}\] là một đường cong parabol đi qua gốc tọa độ \(O\left( {0;0} \right),\) nhận trục Oy làm trục đối xứng, nằm phía dưới trục hoành, điểm O là điểm cao nhất của đồ thị.

2.Tìm tham số thực m để đồ thị hàm số \[y =  - 2{x^2}\] và đường thẳng \[y = x - m\,\] có điểm chung.

Phương trình hoành độ giao điểm của đồ thị hàm số \[y =  - 2{x^2}\] và đường thẳng \[y = x - m\,\] là \( - 2{x^2} = x - m \Leftrightarrow 2{x^2} + x - m = 0\)                    

\(\Delta  = {1^2} - 4.2.\left( { - m} \right) = 1 + 8m.\)

Để đồ thị hàm số \[y =  - 2{x^2}\] và đường thẳng \[y = x - m\,\] có điểm chung thì \(\Delta  \ge 0 \Rightarrow 1 + 8m \ge 0 \Leftrightarrow m \ge  - \frac{1}{8} \cdot \)

Cách 1: Cho phương trình \[3{x^2} + 5x - 1 = 0\] có hai nghiệm \({x_1}\),\({x_2}\). Tính giá trị biểu thức \(T = 6{x_1} - 7{x_1}{x_2} + 6{x_2}\).

Vì \({x_1}\),\({x_2}\)là hai nghiệm của phương trình \[3{x^2} + 5x - 1 = 0\] nên

theo hệ thức Vi-ét thì \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \frac{b}{a} = \frac{{ - 5}}{3}\\{x_1}{x_2} = \frac{c}{a} = \frac{{ - 1}}{3}\end{array} \right.\).

\[T = 6{x_1} - 7{x_1}{x_2} + 6{x_2} = 6\left( {{x_1} + {x_2}} \right) - 7{x_1}{x_2}\]

  \[ = 6\left( {\frac{{ - 5}}{3}} \right) - 7.\left( {\frac{{ - 1}}{3}} \right) = \frac{{ - 23}}{3}\]

Cách 2: Cho phương trình \[3{x^2} + 5x - 1 = 0\] có hai nghiệm \({x_1}\),\({x_2}\). Tính giá trị biểu thức \(T = 6{x_1} - 7{x_1}{x_2} + 6{x_2}\).

3.Giải được hai nghiệm của phương trình \[3{x^2} + 5x - 1 = 0\]

\[{x_1} = \frac{{ - 5 + \sqrt {37} }}{6};{\rm{ }}{x_2} = \frac{{ - 5 - \sqrt {37} }}{6}\]

\[T = 6{x_1} - 7{x_1}{x_2} + 6{x_2} = 6 \cdot \frac{{ - 5 + \sqrt {37} }}{6} - 7 \cdot \frac{{ - 5 + \sqrt {37} }}{6} \cdot \frac{{ - 5 - \sqrt {37} }}{6} + 6 \cdot \frac{{ - 5 - \sqrt {37} }}{6}\]

   \[ = \frac{{ - 23}}{3}\]

1.Tính thời gian để mỗi vòi chảy đầy bể.

Gọi x (phút) là thời gian chỉ riêng vòi thứ nhất chảy đầy bể nước.

       y (phút) là thời gian chỉ riêng vòi thứ hai chảy đầy bể nước.

Điều kiện x, y > 0.

Mỗi phút vòi thứ nhất chảy được \(\frac{1}{x}\,\)(bể nước).

Mỗi phút vòi thứ hai chảy được \(\frac{1}{y}\,\)(bể nước).

Vì cả hai vòi cùng chảy sau 40 phút thì đầy bể nên mỗi phút cả hai vòi cùng chảy được \(\frac{1}{{40}}\,\)(bể nước).

Từ đó ta có phương trình \(\frac{1}{x} + \frac{1}{y} = \frac{1}{{40}}{\rm{  }}\left( 1 \right)\,\)

Khi mở vòi thứ nhất chảy trong 15 phút rồi khóa lại, sau đó mở vòi thứ hai chảy tiếp trong 20 phút thì lúc này lượng nước trong bể chiếm \[\frac{5}{{12}}\] thể tích của bể nước nên ta có phương trình \(15 \cdot \frac{1}{x} + 20 \cdot \frac{1}{y} = \frac{5}{{12}}{\rm{  }}\left( 2 \right)\,\)

Từ (1) và (2) ta có hệ phương trình

 \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{1}{{40}}\\15 \cdot \frac{1}{x} + 20 \cdot \frac{1}{y} = \frac{5}{{12}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{1}{x} = \frac{1}{{60}}\\\frac{1}{y} = \frac{1}{{120}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 60\\y = 120\end{array} \right.\) (thỏa mãn điều kiện)

Vậy nếu mở riêng từng vòi thì thời gian để vòi thứ nhất chảy đầy bể là

60 (phút), thời gian để vòi thứ hai chảy đầy bể là 120 (phút).

2.Tính thể tích của hình nón.

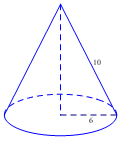
Độ dài đường cao của hình nón là \[h = \sqrt {{l^2} - {r^2}}  = \sqrt {{{10}^2} - {6^2}}  = 8\left( {cm} \right)\]

Thể tích của hình nón là \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.8 = 96\pi \left( {c{m^3}} \right).\)

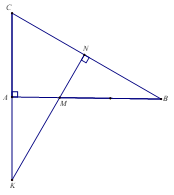
1.Chứng minh tứ giác AMNC nội tiếp.

Xét tứ giác AMNC có

\(\widehat {CAM} = \widehat {CAB} = {90^o}\)(\(\Delta ABC\) vuông tại A, \[M \in AB\]).

\(\widehat {CNM} = {90^o}\) (MN vuông góc BC).

Suy ra \(\widehat {CAM} + \widehat {CNM} = {90^o} + {90^0} = {180^0}\)

Vậy tứ giác AMNC nội tiếp (tổng hai góc đối bằng \({180^0}\)).

2.Chứng minh \(\widehat {ABK} = \widehat {ACM}.\)

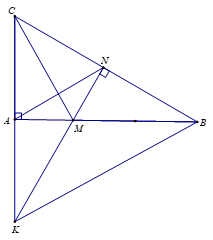
Xét tứ giác ANBK có

\(\widehat {KAB} = {90^o}\) (kề bù với góc vuông CAB).

\(\widehat {KNB} = \widehat {MNB} = {90^o}\) (MN vuông góc BC, K thuộc đường thẳng MN).

Suy ra \(\widehat {KAB} = \widehat {KNB} = {90^o}.\)

Vậy tứ giác ANBK nội tiếp (hai đỉnh A, N kề nhau cùng nhìn cạnh BK dưới một góc bằng \({90^0}\)).

\( \Rightarrow \widehat {ABK} = \widehat {ANK}\)(hai góc nội tiếp cùng chắn cung AK). (1)

Vì tứ giác AMNC nội tiếp (chứng minh câu 5.1)

nên \(\widehat {ANM} = \widehat {ACM}\)(hai góc nội tiếp cùng chắn cung AM).

hay \(\widehat {ANK} = \widehat {ACM}\)(K thuộc đường thẳng MN). (2)

Từ (1) và (2) suy ra \(\widehat {ABK} = \widehat {ACM}.\)

3.Chứng minh \(\frac{1}{r} = \frac{1}{{KN}} + \frac{1}{{CD}} + \frac{1}{{AB}} \cdot \)

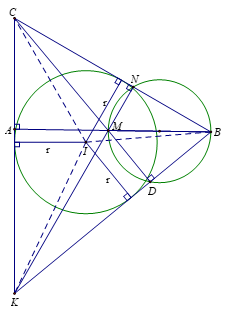
Xét \(\Delta BCK\)có BA là đường cao, KN là đường cao, M là giao điểm của BA và KN.

Suy ra M là trực tâm của \(\Delta BCK.\)

Do đó \(CM \bot BK.\) (1)

Xét đường tròn đường kính BM có \[\widehat {MDB} = {90^0}\] (góc nội tiếp chắn nửa đường tròn).

Suy ra \(MD \bot BK.\)(2)

Từ (1) và (2) suy ra ba điểm C, M, D thẳng hàng. Do đó \(CD \bot BK.\)

Diện tích \[\Delta BIC\]là \[{S_{BIC}} = \frac{1}{2}.r.BC\]

Diện tích \[\Delta BIK\]là \[{S_{BIK}} = \frac{1}{2}.r.BK\]

Diện tích \[\Delta CIK\]là \[{S_{CIK}} = \frac{1}{2}.r.CK\]

Diện tích \[\Delta BCK\]là \[{S_{BCK}} = \frac{1}{2}KN.BC = \frac{1}{2}BK.CD = \frac{1}{2}CK.AB\]

Suy ra \[\frac{1}{2}BC = \frac{{{S_{BCK}}}}{{KN}};{\rm{ }}\frac{1}{2}BK = \frac{{{S_{BCK}}}}{{CD}};{\rm{ }}\frac{1}{2}CK = \frac{{{S_{BCK}}}}{{AB}}\]

Mà \[{S_{BCK}} = {S_{BIC}} + {S_{BIK}} + {S_{CIK}}\]

hay \[{S_{BCK}} = r.\frac{{{S_{BCK}}}}{{KN}} + r.\frac{{{S_{BCK}}}}{{CD}} + r.\frac{{{S_{BCK}}}}{{AB}}\]

  \[ \Rightarrow {S_{BCK}} = r.{S_{BCK}}\left( {\frac{1}{{KN}} + \frac{1}{{CD}} + \frac{1}{{AB}}} \right)\]

Vậy \(\frac{1}{r} = \frac{1}{{KN}} + \frac{1}{{CD}} + \frac{1}{{AB}} \cdot \)