Cho hai đường tròn (0;4)và (0’;3) cắt nhau tại điểm  A,B. Gọi AC,AD lần lượt là các đường kính của (o) và (o’) sao cho AC và AD vuông góc với nhau .

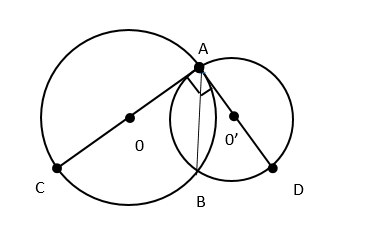
Độ dài BC bằng  : 

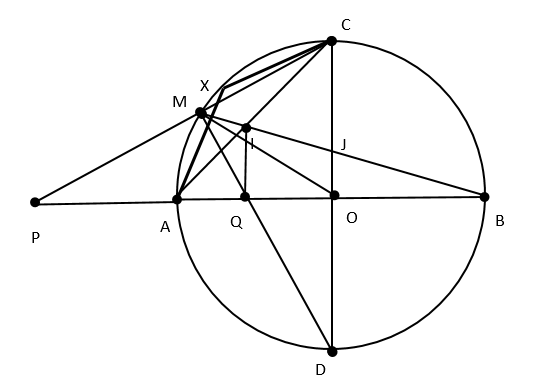
a, do \[AB \bot CD\]tại O nên \[\widehat {POD} = \widehat {BOC} = \widehat {AOC} = {90^0}(1)\]

Xét (O) có \[\widehat {MCD} = {90^0} \Rightarrow DM \bot PC\]TẠI M          \[ \Rightarrow \widehat {PMD} = {90^0}\]

Xét tứ giác OMPD có \[ \Rightarrow \widehat {POD} = \widehat {PMD} = {90^0} \Rightarrow \]TỨ giác OMPD nội tiếp .

b, từ (1) \[ \Rightarrow \] \[\widehat {BOJ} = {90^0}\]

             XÉT (O) có \[\widehat {AMB} = {90^0}\](GOCs nội tiếp chắn nửa đường tròn)

             Xét \[\Delta \]BOJ VÀ  \[\Delta \]BMA có :

              \[\widehat {B{\rm{OJ}}} = \widehat {BMA} = {90^0}\]

               \[\widehat {{\rm{OBJ}}} = \widehat {MBA}\](góc chung)

Do đó \[\Delta B{\rm{OJ}} \sim \Delta BMA\left( {g.g} \right)\] \[ \Rightarrow \frac{{BJ}}{{BO}} = \frac{{BA}}{{BM}} \Rightarrow BJ.BM = BO.BA = R.2R = 2{R^2}\]

c, XÉT (O) có \[\widehat {BMD} = \widehat {BAC}\]( TÍNH CHẤT góc nội tiếp)                                                              \[ \Rightarrow \widehat {IMQ} = \widehat {IAQ}\]

\[ \Rightarrow \]tứ giác AMIQ nội tiếp

\[ \Rightarrow \] \[\widehat {IAQ} + \widehat {AMI} = {180^0} \Rightarrow \widehat {IAQ} + {90^0} = {180^0} \Rightarrow \widehat {IAQ} = {90^0}\]

XÉT \[\Delta AOC\]Có \[\widehat {AOC} = {90^0};OA = OC = R \Rightarrow \Delta AOC\]vuông cân tại O

\[ \Rightarrow \widehat {OAC} = {45^0} \Rightarrow \widehat {IAQ} = {45^0}\]

Xét \[\Delta AQI\]có \[\widehat {AQI} = {90^0};\widehat {IAQ} = {45^0} \Rightarrow \Delta AQI\]vuông cân tại Q

d, tứ giác AOJM nội tiếp nên \[\widehat {MIC} = \widehat {MAQ}\]mà \[\widehat {AMQ} = \widehat {CMB}\](tính chất góc nội tiếp)

do đó \[\Delta MJC \sim \Delta MAQ(g.g) \Rightarrow \frac{{MJ}}{{MC}} = \frac{{MA}}{{MQ}} \Rightarrow MJ.MQ = MA.MC\]

\[{S_{MQJ}} = \frac{1}{2}MJ.MQ.\sin \widehat {MQJ} = \frac{1}{2}MA.MC.\sin {45^0} \le \frac{{\sqrt 2 }}{4}.\frac{{{{\left( {MA + MC} \right)}^2}}}{4}\]

Gọi X là điểm chính giữa của cung nhỏ AC \[ \Rightarrow \]MA+MC\[ \le \]XA+XC(không đổi)

\[{S_{MQJ}} \le \frac{{\sqrt 2 }}{4}.\frac{{{{\left( {XA + XC} \right)}^2}}}{4} = \frac{{{R^2}\left( {\sqrt 2  - 1} \right)}}{2}\](không đổi)

Dấu bằng xảy ra khi \[M \equiv X\]\[ \Rightarrow \]M là điểm chính giữa cung nhỏ AC.

Vậy \[\max {S_{MQJ}} = \frac{{{R^2}\left( {\sqrt 2  - 1} \right)}}{2}\]. Khi M là điểm chính giữa cung nhỏ AC.