PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Giả sử lợi nhuận (tính bằng nghìn đồng) của một quán cà phê nhỏ trong ngày thứ \(x\) của một tháng được cho bởi công thức \(h(x) = - 2{x^2} + 40x + 700\). Trong đó \(x\) là số ngày tính từ ngày đầu tiên của tháng. Do vào đầu tháng, quán bắt đầu có chương trình ưu đãi nên lượng khách tăng nhanh, sau đó lợi nhuận đạt đỉnh rồi giảm dần về cuối tháng. Giả sử tháng đó có 30 ngày. Hỏi, trong bao nhiêu ngày của tháng, lợi nhuận của quán cà phê tăng so với ngày liền trước?
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Giả sử lợi nhuận (tính bằng nghìn đồng) của một quán cà phê nhỏ trong ngày thứ \(x\) của một tháng được cho bởi công thức \(h(x) = - 2{x^2} + 40x + 700\). Trong đó \(x\) là số ngày tính từ ngày đầu tiên của tháng. Do vào đầu tháng, quán bắt đầu có chương trình ưu đãi nên lượng khách tăng nhanh, sau đó lợi nhuận đạt đỉnh rồi giảm dần về cuối tháng. Giả sử tháng đó có 30 ngày. Hỏi, trong bao nhiêu ngày của tháng, lợi nhuận của quán cà phê tăng so với ngày liền trước?
Quảng cáo
Trả lời:
Đáp án:
Đáp án: 9
ĐK: \(x \in \mathbb{N}:1 \le x \le 30\).
Ta có: \(h'(x) = - 4x + 40\)\( \Rightarrow h'(x) = - 4x + 40 = 0 \Leftrightarrow x = 10\).
BBT:
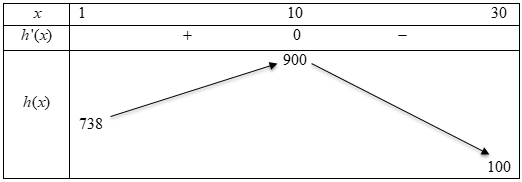
Vậy lợi nhuận của quán cà phê tăng so với ngày liền trước diễn ra trong số ngày là \(10 - 1 = 9\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 1800.
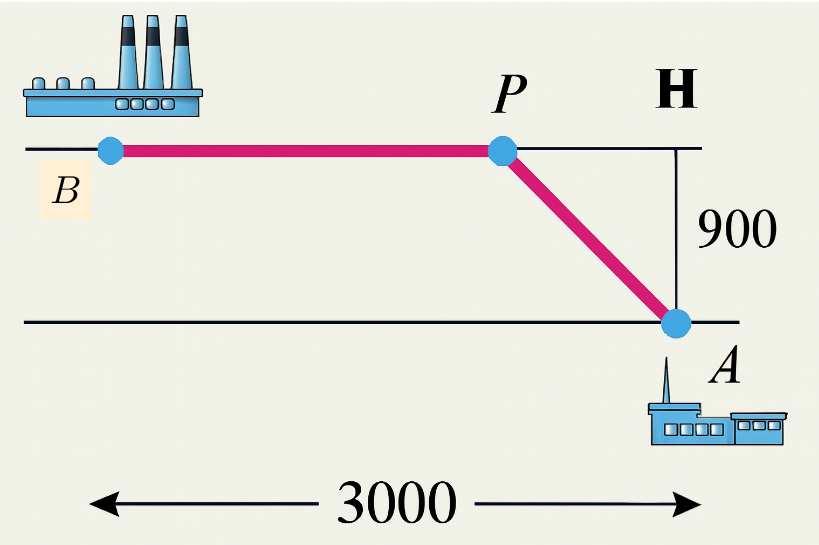
Đặt \(PH = x\,\,\left( {0 \le x \le 3000} \right)\)\( \Rightarrow \)\(PA = \sqrt {{x^2} + {{900}^2}} ;\,\,BP = 3000 - x\).
Do tỉ lệ giữa chi phí để kéo \(1\) mét cáp dưới nước và chi phí kéo \(1\) mét cáp trên bờ bằng \(1,25\)nên tổng chi phí đường cáp điện được kéo từ một trạm điện \(A\) đến một nhà máy \(B\) là
\(f\left( x \right) = PA.1,25 + PB = \sqrt {{x^2} + {{900}^2}} .1,25 + 3000 - x\) với \(0 \le x \le 3000\).
Ta có \(f'\left( x \right) = 1,25.\frac{x}{{\sqrt {{x^2} + {{900}^2}} }} - 1 = \frac{{1,25x - \sqrt {{x^2} + {{900}^2}} }}{{\sqrt {{x^2} + {{900}^2}} }}\).
\(f'\left( x \right) = 0 \Leftrightarrow \sqrt {{x^2} + {{900}^2}} = 1,25x \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} + {900^2} = 1,5625{x^2}\end{array} \right. \Leftrightarrow x = 1200\).
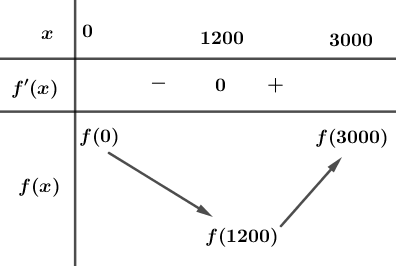
Vậy để tiết kiệm chi phí nhất thì vị trí \(P\) cách nhà máy \(B\) một đoạn bằng \(3000 - 1200 = 1800\,\,\,m\)
Lời giải
Đáp án: 63.
Chi phí vật liệu khi được chiết khấu: \(C\left( x \right) = \left( {1 - 5\% } \right)H\left( x \right) = 47,5{x^2} + 1900x + 47500\) đồng.
Lợi nhuận: \(L\left( x \right) = F\left( x \right) - xG\left( x \right) - C\left( x \right) = - 48,5{x^2} + 6100x - \frac{{100000x}}{{2x + 5}} + 52500\) với \(x \in \left[ {0,400} \right]\)
\( \Rightarrow L'\left( x \right) = - 97x + 6100 + \frac{{500000}}{{{{\left( {2x + 5} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x \simeq - 6,8\\x \simeq 2,1\\x \simeq 62,58\end{array} \right.\).
\(L\left( 0 \right) = 52500,L\left( {2,1} \right) \simeq 42270,L\left( {62,58} \right) \simeq 196220,28,L\left( {400} \right) = - 531789\)
\( \Rightarrow MaxL\left( x \right) = L\left( {62,58} \right) = 196220,28\) khi \(x \simeq 62,8 \simeq 63\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.