Công ty VinaElectro sản xuất một loại thiết bị điện tử tiêu dùng và đánh số seri cho từng sản phẩm bằng một mã 6 chữ số được tạo ngẫu nhiên từ các chữ số \(0,1,2,3,4,5,6,7,8,9\) và chữ số đầu tiên không được là 0. Trong một chương trình khuyến mãi nhân dịp ra mắt sản phẩm mới, công ty muốn tặng quà cho khách hàng nếu sản phẩm họ mua có mã seri “đặc biệt” - là mã số có tích các chữ số bằng 1400. Biết xác suất để khách hàng được tặng quà (tức có mã “đặc biệt”) là \(\frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản và \(a,b \in {\mathbb{N}^*}\). Tính \(b - a\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
1499
Đáp án: 1499
Số phần tử của không gian mẫu bằng \(n\left( \Omega \right) = {9.10^5}\).
Gọi \(A\) là biến cố “Mã số có tích các chữ số bằng 1400”.
Xét \(\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} \) là mã số thuộc biến cố \(A.\)
Ta có \(1400 = {2^3}{.5^2}{.7^1}\), chỉ có các ước trong tập \(\left\{ {0;1;2;...;9} \right\}\) là \(1;2;4;5;7;8\) nên trong các số \({a_1};{a_2};{a_3};{a_4};{a_5};{a_6}\)chỉ có các trường hợp sau:
Trường hợp 1: Có 3 chữ số 2; 2 chữ số 5 và 1 chữ số 7: Chọn 3 vị trí trong các vị trí \({a_1};{a_2};{a_3};{a_4};{a_5};{a_6}\) để cho bằng số 2 có \(C_6^3\) cách; chọn 2 vị trí trong các vị trí \({a_1};{a_2};{a_3};{a_4};{a_5};{a_6}\) để cho bằng số 5 có \(C_3^2\) cách. Vị trí còn lại ta cho bằng 7. Như vậy sẽ có \(C_6^3.C_3^2\) mã số ở trường hợp này.
Trường hợp 2: Có 1 chữ số 2, 1 chữ số 4, 2 chữ số 5, 1 chữ số 7 và 1 chữ số 1: Chọn 2 vị trí trong các vị trí \({a_1};{a_2};{a_3};{a_4};{a_5};{a_6}\) để cho bằng 5 có \[C_6^2\] cách. 4 vị trí còn lại điền đủ các chữ số 1,2,4,7 nên có đúng 4! cách điền cho 4 vị trí còn lại. Số mã số tương ứng trong trường hợp này là \(4!.C_6^2\) .
Trường hợp 3: Có 1 chữ số 8, 1 chữ số 7, 2 chữ số 5, 2 chữ số 1: Chọn ra 2 vị trí để cho bằng 5 có \(C_6^2\) cách; chọn ra 2 vị trí để cho bằng 1 có \(C_4^2\) cách. Hai vị trí còn lại điền hai số 8,7 nên có 2 cách điền số ở hai vị trí còn lại. Số mã số tương ứng trong trường hợp này là \(C_6^2.C_4^2.2\)
Như vậy số phần tử của biến cố \(A\) là \(n\left( A \right) = C_6^3.C_3^2 + C_6^2.4! + C_6^2.C_4^2.2 = 600.\)
Vậy nên xác suất để chọn ra một mã số có tích của tất cả các chữ số bằng 1400 là: \(P\left( A \right) = \frac{{600}}{{{{9.10}^5}}} = \frac{1}{{1500}}\)
Ta có được \(b = 1500;a = 1 \Rightarrow b - a = 1499.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 1800.
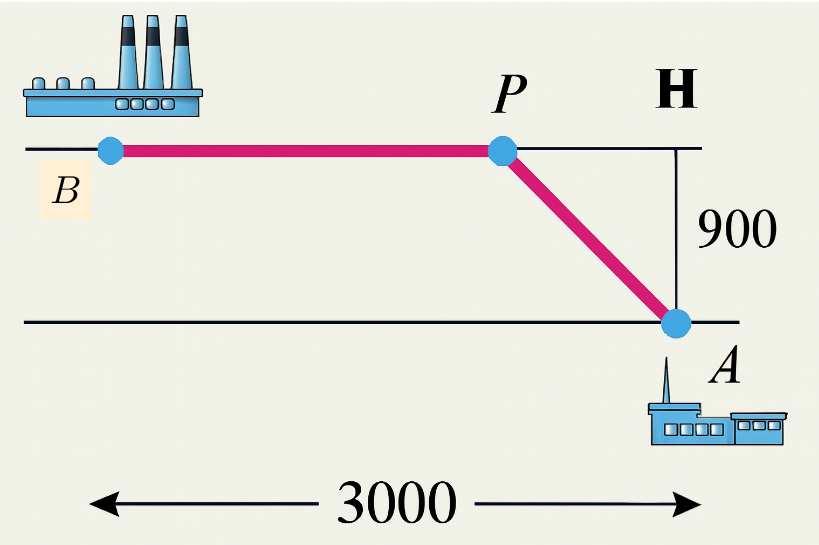
Đặt \(PH = x\,\,\left( {0 \le x \le 3000} \right)\)\( \Rightarrow \)\(PA = \sqrt {{x^2} + {{900}^2}} ;\,\,BP = 3000 - x\).
Do tỉ lệ giữa chi phí để kéo \(1\) mét cáp dưới nước và chi phí kéo \(1\) mét cáp trên bờ bằng \(1,25\)nên tổng chi phí đường cáp điện được kéo từ một trạm điện \(A\) đến một nhà máy \(B\) là
\(f\left( x \right) = PA.1,25 + PB = \sqrt {{x^2} + {{900}^2}} .1,25 + 3000 - x\) với \(0 \le x \le 3000\).
Ta có \(f'\left( x \right) = 1,25.\frac{x}{{\sqrt {{x^2} + {{900}^2}} }} - 1 = \frac{{1,25x - \sqrt {{x^2} + {{900}^2}} }}{{\sqrt {{x^2} + {{900}^2}} }}\).
\(f'\left( x \right) = 0 \Leftrightarrow \sqrt {{x^2} + {{900}^2}} = 1,25x \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} + {900^2} = 1,5625{x^2}\end{array} \right. \Leftrightarrow x = 1200\).
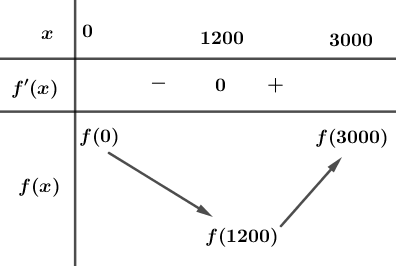
Vậy để tiết kiệm chi phí nhất thì vị trí \(P\) cách nhà máy \(B\) một đoạn bằng \(3000 - 1200 = 1800\,\,\,m\)
Lời giải
Đáp án: 63.
Chi phí vật liệu khi được chiết khấu: \(C\left( x \right) = \left( {1 - 5\% } \right)H\left( x \right) = 47,5{x^2} + 1900x + 47500\) đồng.
Lợi nhuận: \(L\left( x \right) = F\left( x \right) - xG\left( x \right) - C\left( x \right) = - 48,5{x^2} + 6100x - \frac{{100000x}}{{2x + 5}} + 52500\) với \(x \in \left[ {0,400} \right]\)
\( \Rightarrow L'\left( x \right) = - 97x + 6100 + \frac{{500000}}{{{{\left( {2x + 5} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x \simeq - 6,8\\x \simeq 2,1\\x \simeq 62,58\end{array} \right.\).
\(L\left( 0 \right) = 52500,L\left( {2,1} \right) \simeq 42270,L\left( {62,58} \right) \simeq 196220,28,L\left( {400} \right) = - 531789\)
\( \Rightarrow MaxL\left( x \right) = L\left( {62,58} \right) = 196220,28\) khi \(x \simeq 62,8 \simeq 63\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) [NB] Trong khoảng thời gian \[8\] giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của xe là \[26\left( {m/s} \right)\].
Đúng
Sai
b) [TH] Vận tốc của xe tại thời điểm \[t = 3\left( s \right)\] là \[21\left( {m/s} \right)\].
Đúng
Sai
c) [TH] Quãng đường mà xe đi được trong \[8\] giây đầu tiên (làm tròn đến hàng đơn vị) là \[157\left( m \right)\].
Đúng
Sai
d) [VD, VDC] Trong thời gian từ \[0 \le t \le 10\] giây, có thời điểm xe dừng lại.
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) [NB] Hàm số \[f\left( x \right)\] nghịch biến trên khoảng \[\left( { - 1;1} \right)\].
Đúng
Sai
b) [TH] Trên đoạn \[\left[ { - 2;2} \right]\], hàm số \[f\left( x \right)\] đạt giá trị lớn nhất bằng 2.
Đúng
Sai
c) [TH] Hàm số \[f\left( x \right)\] có hai điểm cực trị.
Đúng
Sai
d) [VD,VDC] \[f\left( x \right) = {x^3} - 3x + 1\].
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập