Một chiếc máy đo đạc trắc địa được đặt trên một giá đỡ ba chân. Trọng lực tác dụng lên chiếc máy có độ lớn là \(30{\rm{N}}\) và được phân bố thành ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) lên ba chân của giá đỡ. Ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) có độ lớn bằng nhau và góc tạo bởi mỗi chân của giá đỡ với mặt đất là \(60^\circ \). Hỏi độ lớn của lực \(\overrightarrow {{F_1}} \) là bao nhiêu \({\rm{N}}\) (làm tròn kết quả đến hàng phần chục)?

Một chiếc máy đo đạc trắc địa được đặt trên một giá đỡ ba chân. Trọng lực tác dụng lên chiếc máy có độ lớn là \(30{\rm{N}}\) và được phân bố thành ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) lên ba chân của giá đỡ. Ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) có độ lớn bằng nhau và góc tạo bởi mỗi chân của giá đỡ với mặt đất là \(60^\circ \). Hỏi độ lớn của lực \(\overrightarrow {{F_1}} \) là bao nhiêu \({\rm{N}}\) (làm tròn kết quả đến hàng phần chục)?

Quảng cáo
Trả lời:
Đáp án:
Lời giải
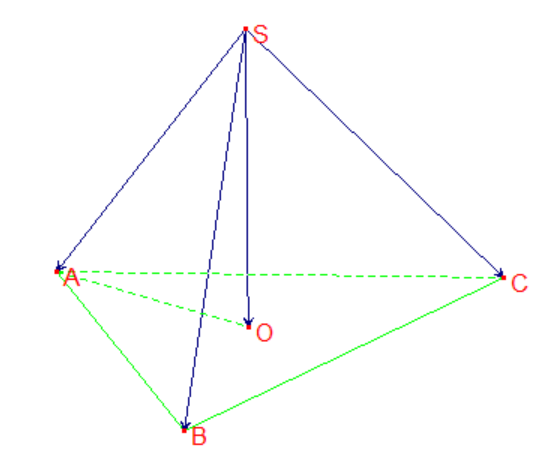
Đáp án: 11,5
Mô hình hóa bài toán bởi ba vec tơ \(\overrightarrow {SA} = \overrightarrow {{F_1}} ;\,\,\,\overrightarrow {SB} = \overrightarrow {{F_2}} ;\,\,\overrightarrow {SC} = \overrightarrow {{F_3}} \) trong đó \(S.ABC\) là hình chóp tam giác đều với \(O\) là tâm của tam giác đều \(ABC\).
Từ giải thiết suy ra \[\left| {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right| = 3\left| {\overrightarrow {SO} } \right| = 30\] nên \(SO = 10.\)
Kết hợp \(\widehat {SAO} = 60^\circ \), suy ra \(SA = \frac{{SO}}{{\sin 60^\circ }} = \frac{{20\sqrt 3 }}{3} \approx 11,5\)
Vậy độ lớn lực \(\overrightarrow {{F_1}} \) là \(11,5\) N.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Lời giải
a) Ta có:
* Chi phí xuất bản \[x\]cuốn tạp chí là \(C\left( x \right)\): \(C\left( x \right) = 0,0001{x^2} - 0,2x + 10000\) (vạn đồng).
* Chi phí phát hành\[x\]cuốn tạp chí là \(H\left( x \right)\): \(H\left( x \right) = 0,4x\) (vạn đồng).
Tổng chi phí \(T\left( x \right)\) (xuất bản và phát hành) cho \(x\) cuốn tạp chí là
\(T\left( x \right) = C\left( x \right) + H\left( x \right)\)
\(T\left( x \right) = \left( {0,0001{x^2} - 0,2x + 10000} \right) + 0,4x\)
\(T\left( x \right) = 0,0001{x^2} + 0,2x + 10000\) vạn đồng.
Mệnh đề a) là ĐÚNG.
b) Số tiền lãi \(L\left( x \right)\) khi in \(x\) cuốn tạp chí bằng Tổng số tiền doanh thu trừ đi tổng số tiền chi phí
Ta tìm hàm doanh thu:
Giá bán \(20\) nghìn đồng/cuốn \( = 2\) vạn đồng/cuốn.
Doanh thu từ bán \(x\) cuốn: \(2x\) (vạn đồng).
Khoản trợ giúp: \(90\) triệu đồng \( = 9000\) vạn đồng.
Tổng doanh thu \(R\left( x \right)\) là: \(R\left( x \right) = 2x + 9000\) (vạn đồng)
Số tiền lãi \(L\left( x \right)\) khi in \(x\) cuốn tạp chí là \(L\left( x \right) = R\left( x \right) - T\left( x \right)\)
\(L\left( x \right) = \left( {2x + 9000} \right) - \left( {0,0001{x^2} + 0,2x + 10000} \right)\)
\(L\left( x \right) = - 0,0001{x^2} + \left( {2 - 0,2} \right)x + \left( {9000 - 10000} \right)\)
\(L\left( x \right) = - 0,0001{x^2} + 1,8x - 1000\)
Mệnh đề b) là SAI
c) Để có lãi cần in bao nhiêu cuốn
Để có lãi, ta cần \(L\left( x \right) > 0\).
\( - 0,0001{x^2} + 1,8x - 1000 > 0 \Leftrightarrow \)\(573,85 < x < 17426.14\)
Vậy, để có lãi (in ra số nguyên cuốn), cần in từ \(574\) đến \(17426\) cuốn.
Mệnh đề c) là ĐÚNG
d) Hàm lãi \(L\left( x \right) = - 0,0001{x^2} + 1,8x - 1000\) là một parabol có hệ số \(a = - 0,0001 < 0\), nên hàm số đạt giá trị lớn nhất tại đỉnh của parabol.
\({x_{{\rm{max}}}} = - \frac{b}{{2a}} = - \frac{{1,8}}{{ - 0,0002}} = 9000\)
Lãi lớn nhất đạt được khi in \(9000\) cuốn.
Mệnh đề d) là SAI.
Lời giải
Lời giải
Đáp án: 0,75
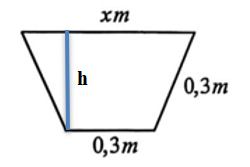
Ta có \(0 < x < 0,9\). Gọi \(h\) là chiều cao của hình thang cân ta có \(h = \sqrt {0,{3^2} - {{\left( {\frac{x}{2} - \frac{{0,3}}{2}} \right)}^2}} = \frac{{\sqrt { - 100{x^2} + 60x + 27} }}{{20}}\)
Diện tích đáy là
\[S\left( x \right) = \frac{1}{2}\left( {0,3 + x} \right)\frac{{\sqrt { - 100{x^2} + 60x + 27} }}{{20}} = \frac{1}{{400}}\left( {3 + 10x} \right)\sqrt { - 100{x^2} + 60x + 27} \].
\[\begin{array}{l}S'\left( x \right) = \frac{1}{{400}}\left[ {10\sqrt { - 100{x^2} + 60x + 27} + \left( {3 + 10x} \right)\frac{{ - 200x + 60}}{{2\sqrt { - 100{x^2} + 60x + 27} }}} \right]\\ = \frac{1}{{40}}\left[ {\frac{{ - 100{x^2} + 60x + 27 + \left( {3 + 10x} \right)\left( { - 10x + 3} \right)}}{{\sqrt { - 100{x^2} + 60x + 27} }}} \right] = \frac{{ - 200{x^2} + 60x + 36}}{{40\sqrt { - 100{x^2} + 60x + 27} }}\\S'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 0,15\\x = 0,75\end{array} \right.\end{array}\]
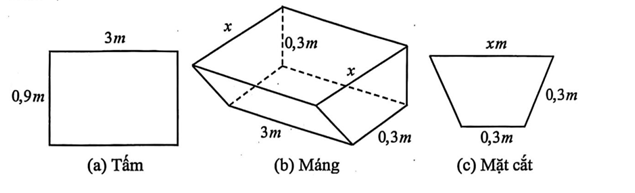
Do chiều cao của máng là 3 m không đổi suy ra thể tích máng lớn nhất khi diện tích đáy lớn nhất.
Vậy \(x = 0,75\left( m \right)\) thì thể tích máng xối lớn nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Lời giải Chọn D Từ đồ thị ta có giá trị lớn nhất của hàm số trên \(\left[ { - 1;3} \right]\) bằng \(3\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/4-1766978932.png)