Một tiệm nước trái cây có kế hoạch làm hai loại nước trái cây để bán cho khách hàng mỗi ngày. Biết rằng mỗi loại nước trái cây đều cần ba loại trái cây là táo, cam và dứa. Để làm 1 kg nước trái cây loại I cần 2 kg táo, 1 kg cam và 4 kg dứa. Để làm 1 kg nước trái cây loại II cần 3 kg táo, 4 kg cam và 1 kg dứa. Biết rằng trong một ngày, cửa hàng đó có thể sử dụng tối đa 120 kg táo, 120 kg cam và 150 kg dứa. Giả sử lợi nhuận của mỗi kg nước bán ra của hai loại đều bằng 70000 đồng/kg, và tiệm có thể bán hết lượng nước sản xuất trong một ngày. Khi đó, lợi nhuận lớn nhất trong một ngày của tiệm là:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là B
Phương pháp giải
Đưa về hệ bất phương trình bậc nhất hai ẩn.
Lời giải
Gọi số kg nước trái cây loại I và loại II mà tiệm sẽ sản xuất trong một ngày lần lượt là \(x,y\left( {x,y \ge 0} \right)\).
Khi đó, lượng táo, cam và dứa mà cửa hàng sẽ sử dụng lần lượt là \(2x + 3y,\,\,x + 4y,\,\,4x + y\left( {{\rm{kg}}} \right)\).
Do trong một ngày, cửa hàng đó có thể sử dụng tối đa 120 kg táo, 120 kg cam và 150 kg dứa, nên ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x \ge 0,y \ge 0}\\{2x + 3y \le 120}\\{x + 4y \le 120}\\{4x + y \le 150}\end{array}} \right.\).
Khi đó, biểu diễn hệ bất phương trình trên trên hệ toạ độ \(Oxy\), ta được miền nghiệm của hệ là miền đa giác với các đỉnh \(O\left( {0;0} \right),A\left( {0;30} \right),B\left( {24;24} \right),C\left( {33;18} \right),D\left( {37,5;0} \right)\).
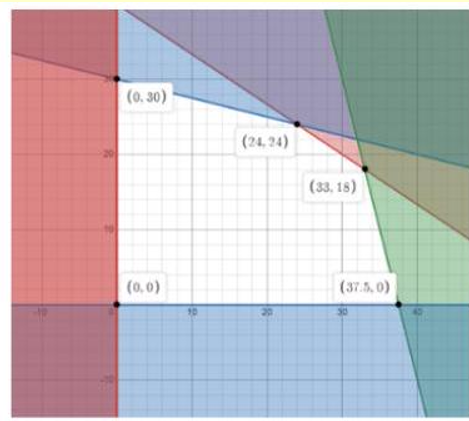
Lợi nhuận của quán trong một ngày sẽ là \(L\left( {x;y} \right) = 70000\left( {x + y} \right)\) (đồng).
\(\begin{array}{l}L\left( O \right) = 0\\L\left( A \right) = 70000\left( {0 + 30} \right) = 2100000\\L\left( B \right) = 70000\left( {24 + 24} \right) = 3360000\\L\left( C \right) = 70000\left( {33 + 18} \right) = 3570000\\L\left( D \right) = 70000\left( {37,5 + 0} \right) = 2625000\end{array}\)
Khi đó, ta xác định được lợi nhuận tối đa của quán trong một ngày là 3570000 đồng khi lựa chọn sản xuất 33 kg nước loại I và 18 kg nước loại II.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là C
Phương pháp giải
Vận dụng lí thuyết về dòng điện xoay chiều
Lời giải
Ta có: Trong 1 chu kỳ, dòng điện có giá trị tức thời bằng giá trị hiệu dụng của nó 2 lần
Vậy trong 50 chu kỳ, dòng điện có giá trị tức thời bằng giá trị hiệu dụng của nó 100 lần.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là B
Phương pháp giải
Vận dụng công thức tính động năng: \({W_d} = \frac{1}{2}m{v^2}\)
Vận dụng lí thuyết về công.
Lời giải
Xét hệ gồm đạn và tấm thép:
- Khi viên đạn xuyên qua tấm thép thì tấm thép tác dụng vào viên đạn một lực F, lực này sinh công làm giảm động năng của viên đạn. Về độ lớn, công của lực F bằng độ giảm động năng của đạn. Ta có: \(A = {W_{0d}} - {W_d} = \frac{1}{2}mv_0^2 - \frac{1}{2}m{v^2} = \frac{1}{2}m\left( {v_0^2 - {v^2}} \right)\)
- Theo nguyên lí I của Nhiệt động lực học: \(\Delta U = Q + A\)
- Vì Q = 0 nên \(\Delta U = A = \frac{1}{2}m\left( {v_0^2 - {v^2}} \right) = \frac{1}{2}0,05\left( {{{100}^2} - {{20}^2}} \right) = 240J\)
- Vì \(\Delta U = 240J > 0\), nên nội năng của hệ (gồm đạn và tấm thép) tăng thêm một lượng là 240J.
Câu 3
C. Tỉ lệ gia tăng dân số tự nhiên Bun-ga-ri cao hơn Cộng hòa Nam Phi.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập